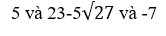Lời giải:
$2-\sqrt{3}=\frac{2^2-3}{2+\sqrt{3}}=\frac{1}{2+\sqrt{3}}$
$3-2\sqrt{2}=\frac{3^2-(2\sqrt{2})^2}{3+2\sqrt{2}}=\frac{1}{3+2\sqrt{2}}$
Mà $2+\sqrt{3}< 3+2\sqrt{2}$ (dễ thấy) nên $\frac{1}{2+\sqrt{3}}> \frac{1}{3+2\sqrt{2}}$ hay $2-\sqrt{3}> 3-2\sqrt{2}$






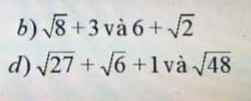
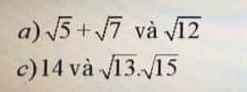

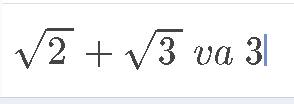 So sánh
So sánh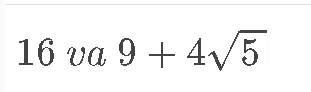 so sánh
so sánh