a=5^120
b= 8^60
vì 5^120= 25^60 >8^60
=> a>b
a=5^120
b= 8^60
vì 5^120= 25^60 >8^60
=> a>b
So sánh hai số : a = 15120 :2560 và b = 245.215.460
Cho a,b,n thuộc Z; b,n>0.
a) Chứng minh: \(\dfrac{a}{b}>1\Leftrightarrow a>b\) và \(\dfrac{a}{b}< 1\Leftrightarrow a< b\)
b) So sánh 2 số hữu tỉ \(\dfrac{a}{b}\) và \(\dfrac{a+1}{b+1}\)
c) So sánh \(\dfrac{a}{b}\) và \(\dfrac{a+n}{a+n}\)
a) Cho a, b , n thuộc Z và b > 0, n > 0
hãy so sánh hai số hữu tỉ a/b và a+n/b+n
Áp dụng kết quả trên hãy so sánh 2/7 và 4/9; -17/25 và -14/28; -31/19 và -21/29.
Cho a, b ∈ Z, b > 0. So sánh 2 số hữu tỉ a b v à a + 2001 b + 2001
Bài 1: So sánh các số sau:(so sánh bằng cách nhanh nhất)
a) -17 và 23 b)-1 và 2 c) 2 và 5 d)267 và -1347
36 -48 3 5 7 4 -268 1343
Bài 2: Tính bằng 2 cách:
5 -(1 3-0,4)
2 7
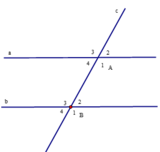
Cho hình vẽ bên, biết a // b và B ^ 2 = 45 0
a). Tính số đo A ^ 1
b). So sánh A ^ 3 và B ^ 1
c). Tính A ^ 2 + B 1 ^
2. So sánh các số hữu tỉ sau bằng cách nhanh nhất
a) 267/ -268 và -1347/1343
b) -13/38 và 29/ -88
3. So sánh a/b (b>0) và a+n/b cộng n ( n thuộc N*)
Bài 1: So sánh các số sau: a/ 2^150 và 3^100 b / 2^24 và 3^16
câu 3:cho a, b thuộc Z và b>0. So sánh 2 số hữu tỉ a/b và a+2001/b+2001
Cho a, b , b>0. So sánh 2 số hữu tỉ a/b và a+2001 / b+2001