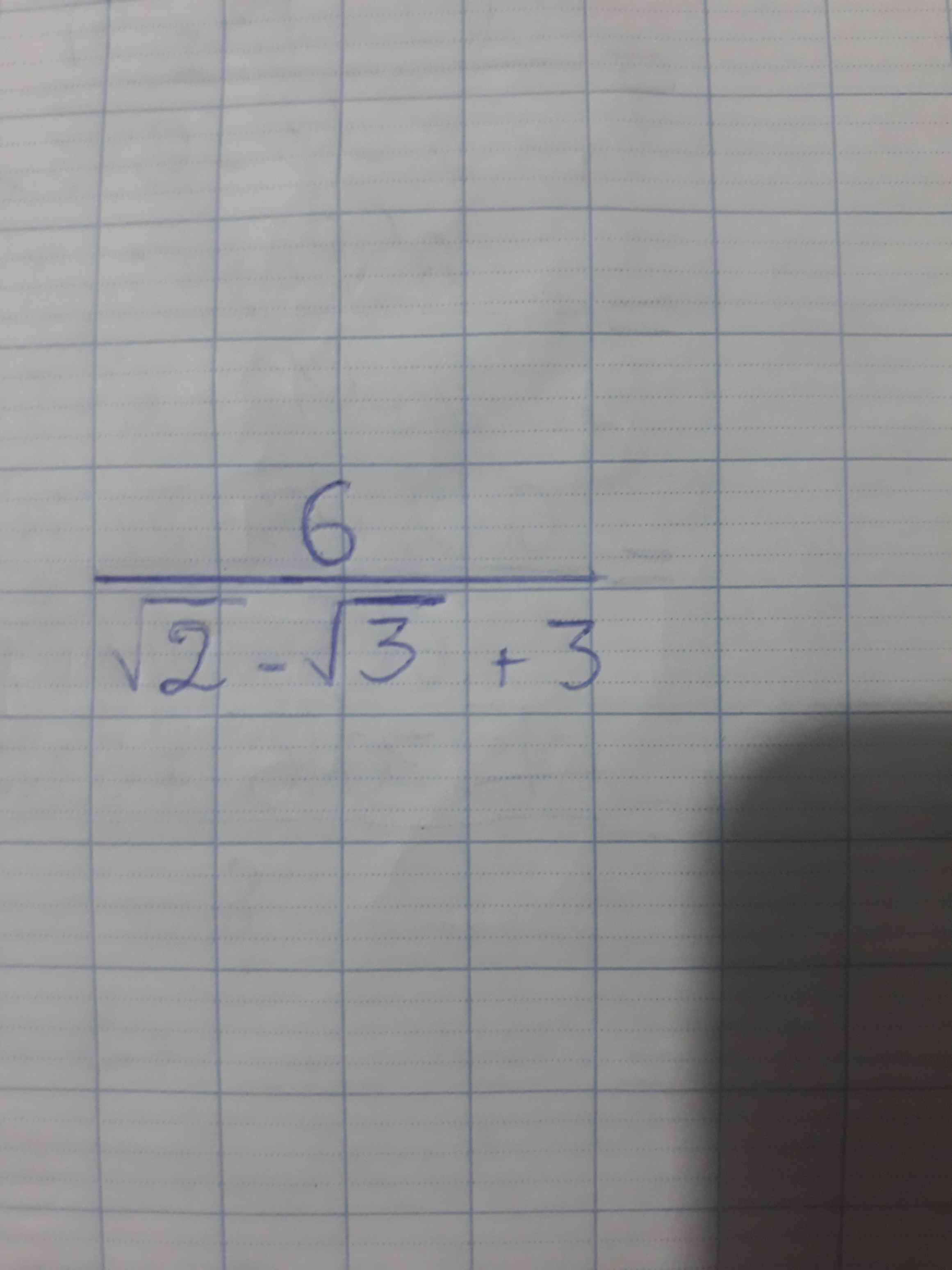\(=\left(\sqrt{5}-\sqrt{3}\right).\sqrt{2}.\sqrt{8-\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right).\sqrt{16-2\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{15-2\sqrt{15}+1}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{15}-1\right)^2}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left|\sqrt{15}-1\right|\)\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{15}-1\right)=5\sqrt{3}-\sqrt{5}-3\sqrt{5}+\sqrt{3}\)
\(=6\sqrt{3}-4\sqrt{5}\)
Vậy...
\(\left(\sqrt{10}-\sqrt{6}\right)\sqrt{8-\sqrt[]{15}}\)
\(=\sqrt{2}\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-\sqrt{15}}\)
\(=\sqrt{16-2\sqrt{15}}.\left(\sqrt{5}-\sqrt{3}\right)=\sqrt{\left(\sqrt{15}-1\right)^2}\left(\sqrt{5}-\sqrt{3}\right)\)
\(=\left(\sqrt{15}-1\right)\left(\sqrt{5}-\sqrt{3}\right)=5\sqrt{3}-3\sqrt{5}-\sqrt{5}+\sqrt{3}=6\sqrt{3}-4\sqrt{5}\)
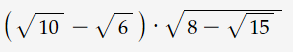
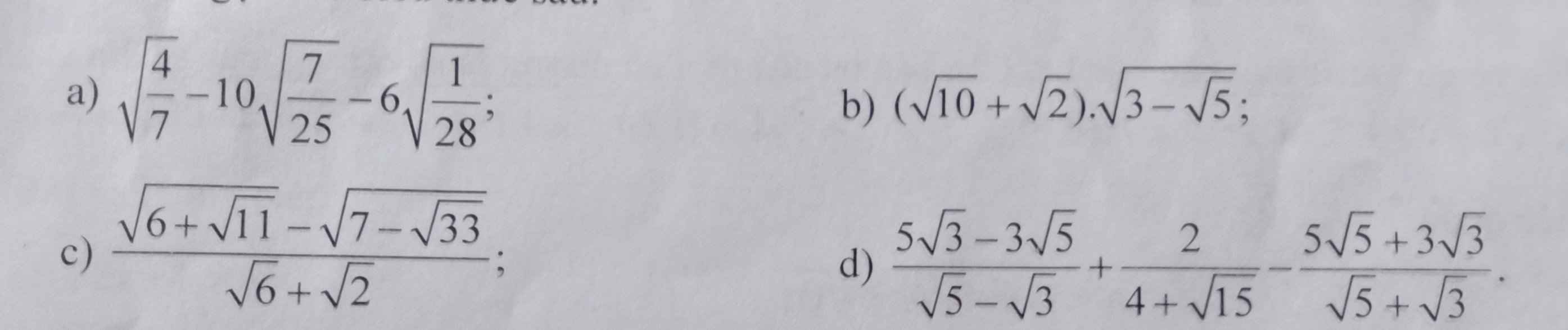rút gọn giúp mình vs ạ 
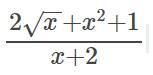Rút gọn giúp mình với ạ
