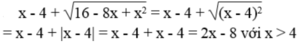Các câu hỏi tương tự
Rút gọn biểu thức N=\(\left(\dfrac{\sqrt{x}}{\sqrt{x}+4}+\dfrac{4}{\sqrt{x}-4}\right):\dfrac{\sqrt{x}+16}{\sqrt{x}+2}\) với x≥0 ; x≠16
Rút gọn biểu thức
4
-
x
+
4
-
x
x
2
-
8
x
+
16
với x 4 là A. 5 - x B. 3 - x C. 3 + x D. x - 4
Đọc tiếp
Rút gọn biểu thức 4 - x + 4 - x x 2 - 8 x + 16 với x < 4 là
A. 5 - x
B. 3 - x
C. 3 + x
D. x - 4
Cho biểu thức : \(A=\frac{\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}}{\sqrt{1-\frac{8}{x}+\frac{16}{x^2}}}\)
Rút gọn rồi tìm các giá trị nguyên của x để A nguyên
\(\frac{\sqrt{x+4\sqrt[]{x-4}}+\sqrt{x-4\sqrt{x+4}}}{\sqrt{1-\frac{8}{x}+\frac{16}{x^2}}}\) rút gọn rồi tìm các gí trị nguyên của x để biểu thức nguyên
rút gọn biểu thức
\(\frac{\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x+4}}}{\frac{16}{x^2}-\frac{8}{x}+1}\)
Cho biểu thức B = 16 x + 16 - 9 x + 9 + 4 x + 4 + x + 1
với x ≥ -1.
Rút gọn biểu thức B;
1 a..Rút gọn biểu thức A = \(\dfrac{\text{ x 2 − 4 x + 4}}{\text{x 3 − 2 x 2 − ( 4 x − 8 ) }}\)
b. Rút gọn biểu thức B = \(\left(\dfrac{x+2}{\text{x }\sqrt{\text{x }}+1}-\dfrac{1}{\sqrt{\text{x}}+1}\right).\dfrac{\text{4 }\sqrt{x}}{3}\)
Cho biểu thức A = \(y=\frac{\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}}{\sqrt{1-\frac{8}{x}+\frac{16}{x^2}}}\)
Rút gọn A, tìm các giá trị nguyên của x để A có giá trị nguyên.
Bài 1: Giải phương trình sau:2x^2+5+2sqrt{x^2+x-2}5sqrt{x-1}+5sqrt{x+2}Bài 2: Cho biểu thứcPleft(frac{6x+4}{3sqrt{3x^2}-8}-frac{sqrt{3x}}{3x+2sqrt{3x}+4}right).left(frac{1+3sqrt{3x^2}}{1+sqrt{3x}}-sqrt{3x}right)a) Tìm ĐKXĐ và rút gọn biểu thức Pb) Tìm tất cả các giá trị nguyên của x để biểu thức P có giá trị nguyênBài 3: Cho biểu thứcAfrac{sqrt{x+4sqrt{x-4}}+sqrt{x-4sqrt{x-4}}}{sqrt{1-frac{8}{x}+frac{16}{x^2}}}a) Tìm ĐKXĐ và rút gọn biểu thức Ab) Tìm tất cả các giá trị nguyên của x để biểu thức...
Đọc tiếp
Bài 1: Giải phương trình sau:
\(2x^2+5+2\sqrt{x^2+x-2}=5\sqrt{x-1}+5\sqrt{x+2}\)
Bài 2: Cho biểu thức
\(P=\left(\frac{6x+4}{3\sqrt{3x^2}-8}-\frac{\sqrt{3x}}{3x+2\sqrt{3x}+4}\right).\left(\frac{1+3\sqrt{3x^2}}{1+\sqrt{3x}}-\sqrt{3x}\right)\)
a) Tìm ĐKXĐ và rút gọn biểu thức P
b) Tìm tất cả các giá trị nguyên của x để biểu thức P có giá trị nguyên
Bài 3: Cho biểu thức
\(A=\frac{\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}}{\sqrt{1-\frac{8}{x}+\frac{16}{x^2}}}\)
a) Tìm ĐKXĐ và rút gọn biểu thức A
b) Tìm tất cả các giá trị nguyên của x để biểu thức A có giá trị nguyên