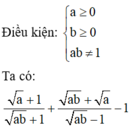Các câu hỏi tương tự
\(\left(\frac{ab+a}{ab-1}+\frac{a+1}{ab-a}-1\right):\left(1-\frac{ab+a}{ab-1}+\frac{a+1}{ab+1}\right)\)
Rút gọn biểu thức
B=\(\left(\frac{\sqrt{a}+1}{\sqrt{ab}+1}+\frac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\right):\left(\frac{\sqrt{a}+1}{\sqrt{ab}+1}-\frac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+-\right)\)Rút gọn biểu thức
Rút gọn biểu thức:
A= \(\left(\frac{\sqrt{a}+1}{\sqrt{ab}+1}+\frac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\right):\left(\frac{\sqrt{a}+1}{\sqrt{ab}+1}-\frac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\right)\)
9 tháng 8 2015 lúc 21:05
Rút gọn biểu thức: \(\left(\frac{\sqrt{a}+1}{\sqrt{ab}+1}+\frac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}\right):\left(\frac{\sqrt{a}+1}{\sqrt{ab+1}}-\frac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\right)\)
10 tháng 10 2023 lúc 19:54
Cho biểu thức:
\(D=\left(\dfrac{\sqrt{a}+\sqrt{b}}{1-\sqrt{ab}}+\dfrac{\sqrt{a}-\sqrt{b}}{1+\sqrt{ab}}\right):\left(1+\dfrac{a+b+2ab}{1-ab}\right)\)
a) Tìm đkxđ và rút gọn \(D\)
b) Tính \(D\) với \(a=\dfrac{2}{2+\sqrt{3}}\)
c) Tìm giá trị lớn nhất của \(D\)
cho biểu thức
P=\(\left(\frac{\sqrt{a}}{\sqrt{ab}}+\frac{\sqrt{ab}+\sqrt{a}}{1-\sqrt{ab}}+1\right):\left(1+\frac{\sqrt{ab}+\sqrt{a}}{1-\sqrt{ab}}-\frac{\sqrt{a}+1}{\sqrt{ab}+1}\right)\\ \\ \\ \)
a) Rút gọn biểu thức
b) Cho \(\frac{1}{\sqrt{a}}+\frac{1}{\sqrt{b}}=6\).Tìm giá trị lớn nhất của P
rút gọn biểu thức a
A= \(\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
a/ rút gọn A
b/ tìm giá trị để A dương
Cho biểu thức: A= \(\left(\dfrac{1}{\sqrt{a}-3}+\dfrac{1}{\sqrt{a}+3}\right)\left(1-\dfrac{3}{\sqrt{a}}\right)\)
a) Rút gọn biểu thức sau A
b) Xác định a để biểu thức A > \(\dfrac{1}{2}\)
Rút gọn biểu thức
a. B = \(\left(\dfrac{a-b}{a^2+ab}-\dfrac{a}{b^2+ab}\right):\left(\dfrac{b^3}{a^3-ab^2}+\dfrac{1}{a+b}\right)\)
b. C = \(a:\left(b-2\right)-\left[\left(a^2+2a+1\right):\left(b^2-4\right)\right].\left[\left(b+2\right):\left(a+1\right)\right]\)