Với `x >= 0, x \ne 4`. Ta có:
`A = [ \sqrt{x} + 2 ] / [ \sqrt{x} - 2 ] - [ \sqrt{x} - 2 ] / [ \sqrt{x} + 2 ] + [4x] / [ x - 4 ]`
`A = [ \sqrt{x} + 2 ] / [ \sqrt{x} - 2 ] - [ \sqrt{x} - 2 ] / [ \sqrt{x} + 2 ] + [4x] / [ ( \sqrt{x} + 2 ) ( \sqrt{x} - 2 ) ]`
`A = [ ( \sqrt{x} + 2 )^2 - ( \sqrt{x} - 2 )^2 + 4x ] / [ ( \sqrt{x} + 2 ) ( \sqrt{x} - 2 ) ]`
`A = [ x + 4\sqrt{x} + 4 - x + 4\sqrt{x} - 4 + 4x ] / [ ( \sqrt{x} + 2 ) ( \sqrt{x} - 2 ) ]`
`A = [ 8\sqrt{x} + 4x ] / [ ( \sqrt{x} + 2 ) ( \sqrt{x} - 2 ) ]`
`A = [ 4\sqrt{x} ( \sqrt{x} + 2 ) ] / [ ( \sqrt{x} + 2 ) ( \sqrt{x} - 2 ) ]`
`A = [4\sqrt{x}] / [ \sqrt{x} - 2 ]`

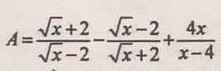









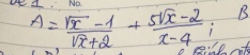


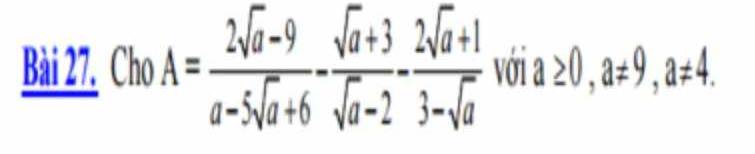 a, rút gọn
a, rút gọn 
