\(c,Sửa:\dfrac{1}{4x+2}=\dfrac{x\left(2x-1\right)}{2x\left(2x+1\right)\left(2x-1\right)}\\ \dfrac{20}{4x^3-x}=\dfrac{40}{2x\left(2x+1\right)\left(2x-1\right)}\\ \dfrac{7}{2x^2+x}=\dfrac{7\left(2x-1\right)}{x\left(2x+1\right)\left(2x-1\right)}\\ d,\dfrac{x}{x-y};\dfrac{x^2-y^2}{x^2-2xy+y^2}=\dfrac{\left(x-y\right)\left(x+y\right)}{\left(x-y\right)^2}=\dfrac{x+y}{x-y};x+y=\dfrac{x^2-y^2}{x-y}\\ e,\dfrac{x}{x+1}=\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)};\dfrac{x^2}{1-x}=\dfrac{-x^2\left(x+1\right)}{\left(x+1\right)\left(x-1\right)};\dfrac{1}{x^2-1}=\dfrac{1}{\left(x-1\right)\left(x+1\right)}\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
phân tích đa thức thành phân tử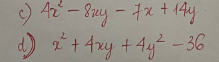 trình bày đầy đủ nha
trình bày đầy đủ nha
phân tích đa thức thành nhân tử x2y+xy2-7x-7y trình bày đầy đủ nha
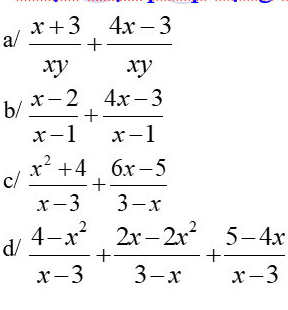 trình bày đầy đủ nha
trình bày đầy đủ nha
trình bày đầy đủ nha
Đọc tiếp
trình bày đầy đủ nha
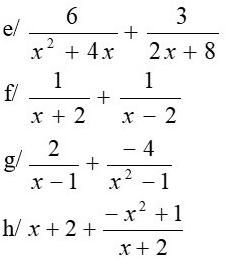 trình bày đầy đủ nha
trình bày đầy đủ nha
trình bày đầy đủ nha
Đọc tiếp
trình bày đầy đủ nha
 trình bày đầy đủ nha
trình bày đầy đủ nha
 trình bày đầy đủ nha
trình bày đầy đủ nha
trình bày đầy đủ nha
Đọc tiếp
trình bày đầy đủ nha




