Thay z = 1 + i vào phương trình đã cho ta có:
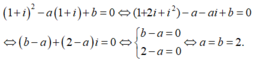
Chọn đáp án B.
Thay z = 1 + i vào phương trình đã cho ta có:
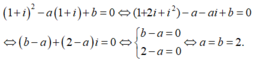
Chọn đáp án B.
Cho phương trình \(z^2+bc+c=0\) có hai nghiệm z1 z2 thỏa mãn z2 - z1 = 4+2i . Gọi A,B là các điểm biểu diễn các nghiệm của phương trình \(z^2-2bz+4c=0\) . Tính độ dài đoạn AB
A: \(8\sqrt{5}\)
B: \(2\sqrt{5}\)
C: \(4\sqrt{5}\)
D: \(\sqrt{5}\)
Cho phương trình \(az^2+bz+c=0\) với a,b,c ∈ R , a ≠ 0 có các nghiệm z1,z2 đều không là số thực . Tính P |z1 +z2|2 + |z1 -z2|2 theo a,b,c
A: P= \(\dfrac{b^2-2ac}{a^2}\)
B: P= \(\dfrac{2c}{a}\)
C: P=\(\dfrac{4c}{a}\)
D: P= \(\dfrac{2b^2-4ac}{a^2}\)
Phương trình \(z^2+az+b=0\) với a b là các số thực nhận số phức 1+i là một nghiệm.Tính a - b?
A:-2
B:-4
C:4
D:0
Phương trình z 2 + a z + b = 0 nhận z = 1 - 2i làm nghiệm. Khi đó a + b bằng
A. 3
B. 4
C. 5
D. 6
Số phức z=a+bi, a,b thuộc R là nghiệm của phương trình ( z - 1 ) ( 1 + i z z - 1 z = i . Tổng T=a^2+b^2 bằng
A. ![]() .
.
B. ![]() .
.
C.![]()
D. ![]() .
.
Phương trình z 1 = 1 + 2 i , z 2 = 2 - 3 i có nghiệm là z = 2 + i khi
A. a = 1, b = 4
B. a = -1, b = 4
C. a = -1, b = -4
D. a = 1, b = -4
Xét các số phức z=a+bi ( a , b ∈ R ) thỏa mãn z - 3 - 2 i = 2 . Tính a+b khi z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
![]()
![]()
![]()
![]()
Cho phương trình z 3 + a z 2 + b z + c = 0 nhận z = 2 và z = 1 + i làm các nghiệm của phương trình. Khi đó a - b + c là
![]()
![]()
![]()
![]()
Cho số phức thỏa mãn: z=a+bi, ( a , b ∈ R ) thỏa mãn: z ( 2 + i ) = z - 1 + i ( 2 z + 3 ) . Tính S = a + b
![]()
![]()
![]()
![]()