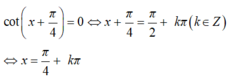Các câu hỏi tương tự
Cho phương trình cos2x.cosx + sinx.cos3x sin2x.sinx - sin3x.cosx và các họ số thực: I. x
π
4
+ kπ, k ∈ Z. II. x
-
π
2
+ k2π, k ∈ Z. III. x
-
π
14
+
k
2
π
7
, k ∈ Z. ...
Đọc tiếp
Cho phương trình cos2x.cosx + sinx.cos3x = sin2x.sinx - sin3x.cosx và các họ số thực:
I. x = π 4 + kπ, k ∈ Z.
II. x = - π 2 + k2π, k ∈ Z.
III. x = - π 14 + k 2 π 7 , k ∈ Z.
IV. x = π 7 + k 4 π 7 , k ∈ Z.
Chọn trả lời đúng: Nghiệm của phương trình là:
A. I, II
B. I, III
C. II, III
D. II, IV.
Tính đạo hàm của hàm số: y = tan π / 2 – x với x ≠ k π , k ∈ Z
Cho hàm số y sin4xa) Chứng minh rằng sin4(x + kπ/2) sin4x với k ∈ ZTừ đó vẽ đồ thị của hàm sốy sin4x; (C1)y sin4x + 1. (C2)b) Xác định giá trị của m để phương trình: sin4x + 1 m (1)- Có nghiệm- Vô nghiệmc) Viết phương trình tiếp tuyến của (C2) tại điểm có hoành độ
x
0
π
/
24
Đọc tiếp
Cho hàm số y = sin4x
a) Chứng minh rằng sin4(x + kπ/2) = sin4x với k ∈ Z
Từ đó vẽ đồ thị của hàm số
y = sin4x; (C1)
y = sin4x + 1. (C2)
b) Xác định giá trị của m để phương trình: sin4x + 1 = m (1)
- Có nghiệm
- Vô nghiệm
c) Viết phương trình tiếp tuyến của (C2) tại điểm có hoành độ x 0 = π / 24
Cho hàm số
y
cos
2
x
.a) Chứng minh rằng cos
2
x
+
k
π
cos
2
x
với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số
y
cos
2
x
.b) Viết phương...
Đọc tiếp
Cho hàm số y = cos 2 x .
a) Chứng minh rằng cos 2 x + k π = cos 2 x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos 2 x .
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π / 3 .
c) Tìm tập xác định của hàm số : z = 1 - cos 2 x 1 + cos 2 2 x
2
cos
3
x
sin
3
x
phương trình đã cho có nghiệm
x
π
4
+
k
π
x...
Đọc tiếp
2 cos 3 x = sin 3 x phương trình đã cho có nghiệm x = π 4 + k π x = a r c t a n + k π k ∈ Z vậy A là:
A.2
B.3
C.4
D.-2
Phương trình tan( x - π/4) = 0 có nghiệm là:
A. x = π/4 + kπ, k ∈ Z.
B. x = 3π/4 + kπ, k ∈ Z.
C. x = kπ, k ∈ Z.
D. x = k2π, k ∈ Z.
Tập nghiệm của phương trình -9sinx+6cosx-3sin2x+cos2x= -10 là: x = a π b + k 2 π ( k ∈ Z ) tính giá trị của a2 – b : (biết a, b tối giản)
A.3
B.-2
C.4
D.-1
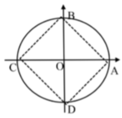
Có 4 họ nghiệm được biểu diễn bởi các điểm A,B,C và D trên đường tròn đơn vị ở hình. Trong đó: Ứng với điểm A là họ nghiệm x 2k
π
Ứng với điểm B là họ nghiệm x
π
2
+
2
k
π
Ứng với điểm C là họ nghiệm x
π
+
2
k
π
Ứng với điểm D là họ nghiệm x
-
π
2
+
2
k...
Đọc tiếp
Có 4 họ nghiệm được biểu diễn bởi các điểm A,B,C và D trên đường tròn đơn vị ở hình. Trong đó:
Ứng với điểm A là họ nghiệm x = 2k π
Ứng với điểm B là họ nghiệm x = π 2 + 2 k π
Ứng với điểm C là họ nghiệm x = π + 2 k π
Ứng với điểm D là họ nghiệm x = - π 2 + 2 k π Phương trình cot3x=cotx có các họ nghiệm được biểu diễn bởi các điểm
A. A và B
B. C và D
C. A và C
D. B và D
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4cos^3 x - cos 2x + (m-3)cos x - 1 = 0 có đúng 4 nghiệm khác nhau thuộc khoảng (-π/2; π/2)