- TH1: Nếu a ≠ 0 thì phương trình có nghiệm duy nhất ⇔ ∆ = 0 .
- TH2: Nếu a = 0 thì phương trình trở thành b x + c = 0 có nghiệm duy nhất ⇔ b ≠ 0
Đáp án cần chọn là: B
Bài 1: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua đường thẳng Δ, với:
a, d: 2x-y+1=0, Δ: 3x-4y+2=0
b, d: x-2y+4=0, Δ: 2x+y-2=0
c, d: x+y-1=0, Δ: x-3y+3=0
d, d: 2x-3y+1=0, Δ: 2x-3y-1=0
Bài 2: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua điểm I với:
a, d: 2x-y+1=0, I(2;1)
b, d: x-2y+4=0, I(-3;0)
c, d: x+y-1=0, I(0:3)
d, d: 2x-3y+1=0, I trùng O(0;0)
GIÚP EM VỚI Ạ!! EM ĐANG CẦN GẤP LẮM HUHUU T^T EM XIN CẢM ƠN!!!
Câu 1.Tìm m để phương trình sau có nghiệm (m - 1)x - 2 = 0.
A. m=1 B. m= - 1 C. m=0 D. m≠ 1
Câu 2. Phương trình \(\left(m^2-4\right)x=3m+6\) có nghiệm duy nhất khi và chỉ khi
A. \(m\ne\pm2;m\ne-3\) B. \(m\ne-2\) C. \(m\ne2\) D. \(m\ne\pm2\)
Đồ thị hàm số y = f ( x ) = a x 2 + b x + c được cho trong hình 47. Kí hiệu Δ = b 2 - 4 a c là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
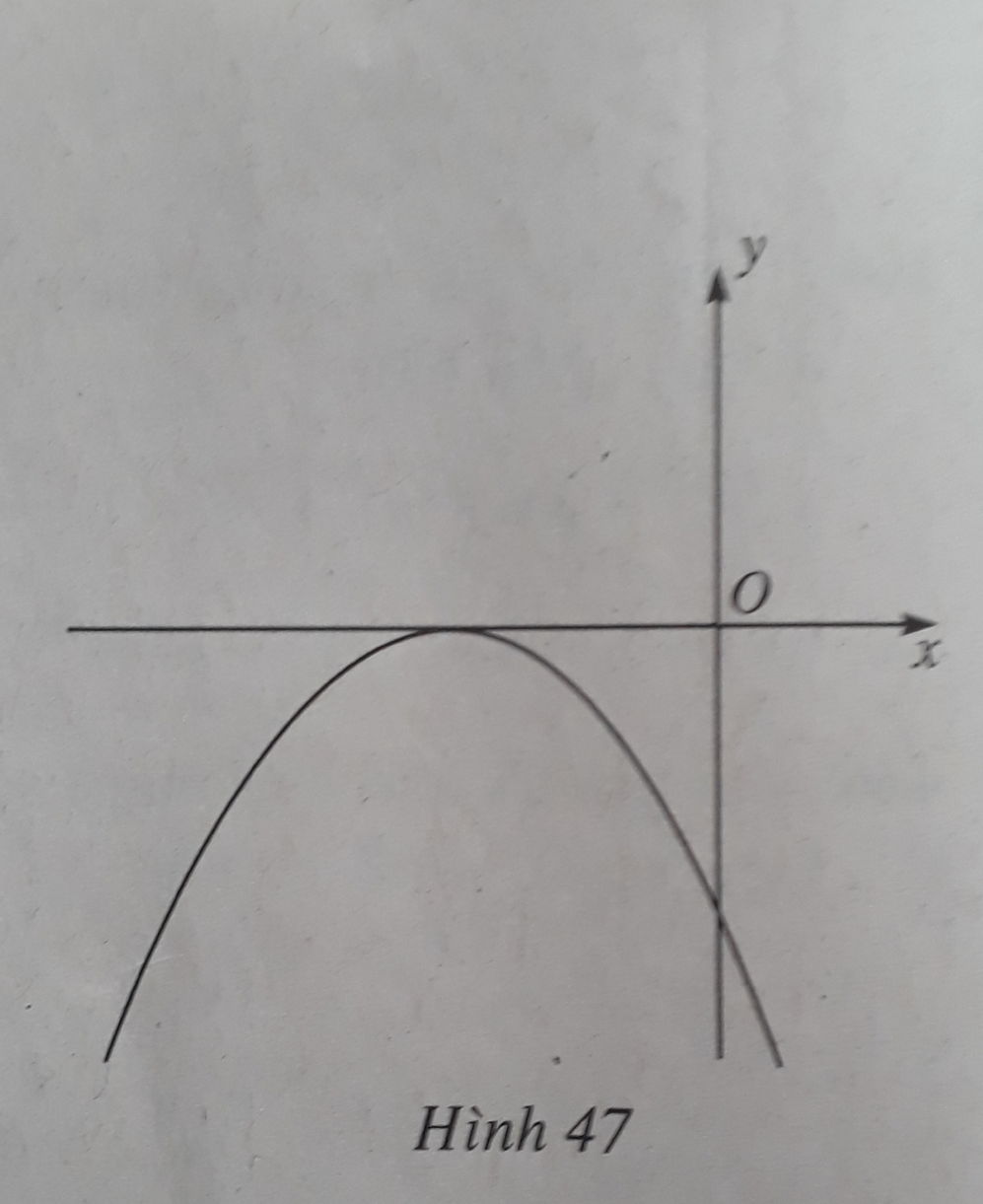
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0).
a, Tìm điểm đối xứng của O qua Δ.
b, Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
a)Viết phương trình đường tròn đi qua 3 điểm A(-1;1);B(3;1);C(1;3)
b)Cho (C):x2+y2-4x+6y+3=0 và (Δ):3x-y+m=0.Tìm m để đường thẳng (Δ) tiếp xúc với đường tròn (C)
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;1),B(4;-2) và đường thẳng d: -x+2y+1=0. a) Viết phương trình tham số của Δ đi qua A song song với đường thẳng d b) Viết phương trình tổng quát của Δ đi qua B và vuông góc với đường thẳng d c) Viết phương trình đường tròn có bán kính AB
Tìm nghiệm của phương trình sau:
A. x = 0 và x = 1 B. x = 1 và x = 2
C. x = 0 và x = 2 D. x = 0 và x = 1
Cho f(x)=x^2 -2(m-2)x+m+10. Định m để:
a. Phương trình f(x)=0 có một nghiệm x= 1 và tính nghiệm kia
b. Phương trình f(x)=0 có nghiệm kép. Tính nghiệm kép đó.
c. Tìm m để phương trình f(x)=0 có 2 nghiệm âm phân biệt.
d. Tìm m để f(x)<0 có nghiệm đúng với mọi xϵR
Tìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau:
a, A(3; 5) và Δ : 4x + 3y +1 = 0
b, B(1; -2) và d: 3x – 4y -26 = 0
c, C(1; 2) và m: 3x + 4y -11 = 0
Nếu a, b, c, d là các số thực khác 0, biết c và d là nghiệm của phương trình x 2 + a x + b = 0 và a, b là nghiệm của phương trình x 2 + c x + d = 0 thì
A. -2
B. 0
C. − 1 + 5 2
D. 2
