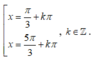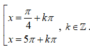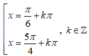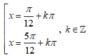Các câu hỏi tương tự
Giải phương trình:
1,\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
2,\(|cosx-sinx|+2sin2x=1\)
3,\(2sin2x-3\sqrt{6}|sinx+cosx|+8=0\)
4,\(cosx+\dfrac{1}{cosx}+sinx+\dfrac{1}{sinx}=\dfrac{10}{3}\)
Phương trình
2
sin
2
x
+
sin
x
cos
x
-
cos
2
x
0
có nghiệm là:
Đọc tiếp
Phương trình 2 sin 2 x + sin x cos x - cos 2 x = 0 có nghiệm là:
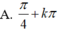


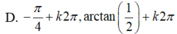
Phương trình 2sin2x + sinx. cosx – cos2x 0 có nghiệm là:
Đọc tiếp
Phương trình 2sin2x + sinx. cosx – cos2x = 0 có nghiệm là:
![]()

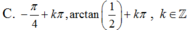
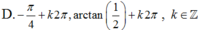
Cho phương trình:
(
sin
x
+
sin
3
x
+
cos
3
x
1
+
2
sin
2
x
)
3
+
cos
2
x
5...
Đọc tiếp
Cho phương trình: ( sin x + sin 3 x + cos 3 x 1 + 2 sin 2 x ) = 3 + cos 2 x 5 . Các nghiệm của phương trình thuộc khoảng ( 0 ; 2 π ) là:
![]()
![]()
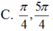
![]()
Cho phương trình:
2
sin
2
x
+
3
sin
2
x
-
2
3
sin
x
+
cos
x
-
m
0
. Để phương trình chỉ có hai nghiệm
x
1
,
x
2...
Đọc tiếp
Cho phương trình: 2 sin 2 x + 3 sin 2 x - 2 3 sin x + cos x - m = 0 . Để phương trình chỉ có hai nghiệm x 1 , x 2 thuộc - π 3 ; π 2 thì m ∈ a ; b . Giá trị b-a là
A. 3 3
B. 4 - 2 3
C. 4
D. 4 3 - 2
Cho phương trình: cos2x+(1+2cosx)(sinx-cosx)=0. Số họ nghiệm của phương trình dạng x = a + k 2 π là:
A.4
B.2
C.1
D.3
Tìm m để phương trình 2sin2x – ( 2m+1) . sinx+ m 0 có nghiệm
x
∈
-
π
2
;
0
A. – 1 m 0 B. 1 m 2 C. – 1 m 0 D. 0 m 1
Đọc tiếp
Tìm m để phương trình 2sin2x – ( 2m+1) . sinx+ m = 0 có nghiệm x ∈ - π 2 ; 0
A. – 1< m < 0
B. 1< m< 2
C. – 1< m< 0
D. 0< m< 1
Tìm m để phương trình 2sin2x – (2m + 1)sinx + m 0 có nghiệm x ∈ (
-
π
2
; 0). A. -1 m B. 1 m C. -1 m 0 D. 0 m 1
Đọc tiếp
Tìm m để phương trình 2sin2x – (2m + 1)sinx + m = 0 có nghiệm x ∈ ( - π 2 ; 0).
A. -1 < m
B. 1 < m
C. -1 < m < 0
D. 0 < m < 1
Tìm nghiệm của phương trình
cos
x
-
3
.
cos
x
2
.
sin
x
-
1
...
Đọc tiếp
Tìm nghiệm của phương trình cos x - 3 . cos x 2 . sin x - 1 = 0
![]()
![]()
![]()
![]()