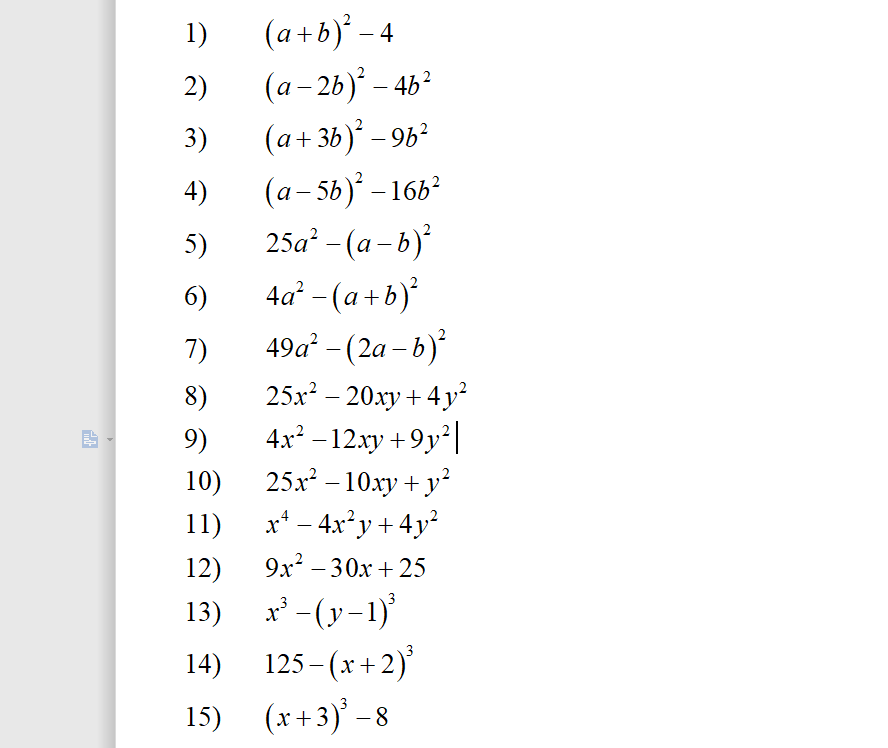
PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
Trong chuyên đề này ta sẽ hệ thống lại các dạng toán và các phương pháp phân tích đa thức thành nhân tử và giải một số bài tập về phân tích đa thức thành nhân tử.
Ta sẽ tìm hiểu về các phương pháp sau:
1. Tách một hạng tử thành nhiều hạng tử
2. Thêm, bớt cùng một hạng tử
3. Đặt ẩn phụ
4. Phương pháp hệ số bất định
I. TÁCH MỘT HẠNG TỬ THÀNH NHIỀU HẠNG TỬ:
Định lí bổ sung:
+ Đa thức f(x)f(x) có nghiệm hữu tỉ thì có dạng pqpq trong đó pp là ước của hệ số tự do, qq là ước dương của hệ số cao nhất
+ Nếu f(x)f(x) có tổng các hệ số bằng 0 thì f(x)f(x) có một nhân tử là x–1x–1
+ Nếu f(x)f(x) có tổng các hệ số của các hạng tử bậc chẵn bằng tổng các hệ số của các hạng tử bậc lẻ thì f(x)f(x) có một nhân tử là x+1x+1
+ Nếu aa là nghiệm nguyên của f(x)f(x) và f(1);f(−1)f(1);f(−1) khác 0 thì f(1)a−1f(1)a−1 và f(−1)a+1f(−1)a+1 đều là số nguyên. Để nhanh chóng loại trừ nghiệm là ước của hệ số tự do
Ví dụ 1: 3x2–8x+43x2–8x+4
Hướng dẫn:
Cách 1: Tách hạng tử thứ 2
3x2–8x+4=3x2–6x–2x+4=3x(x–2)–2(x–2)=(x–2)(3x–2)3x2–8x+4=3x2–6x–2x+4=3x(x–2)–2(x–2)=(x–2)(3x–2)
Cách 2: Tách hạng tử thứ nhất:
3x2–8x+4=(4x2–8x+4)−x2=(2x–2)2–x2=(2x–2+x)(2x–2–x)3x2–8x+4=(4x2–8x+4)−x2=(2x–2)2–x2=(2x–2+x)(2x–2–x)
=(x–2)(3x–2)=(x–2)(3x–2)
Ví dụ 2: x3–x2–4x3–x2–4
Hướng dẫn:
Ta nhận thấy nghiệm của f(x)f(x) nếu có thì x = ±1;±2;±4±1;±2;±4, chỉ có f(2)=0f(2)=0 nên x=2x=2 là nghiệm của f(x)f(x) nên f(x)f(x) có một nhân tử là x–2x–2. Do đó ta tách f(x)f(x) thành các nhóm có xuất hiện một nhân tử là x–2x–2
Cách 1:
x3–x2–4=x3–x2–4= (x3−2x2)+(x2−2x)+(2x−4)(x3−2x2)+(x2−2x)+(2x−4)
=x2(x−2)+x(x−2)+2(x−2)=(x−2)(x2+x+2)=x2(x−2)+x(x−2)+2(x−2)=(x−2)(x2+x+2)
Cách 2:
x3−x2−4=x3−8−x2+4x3−x2−4=x3−8−x2+4
=(x3−8)−(x2−4)=(x−2)(x2+2x+4)−(x−2)(x+2)=(x3−8)−(x2−4)=(x−2)(x2+2x+4)−(x−2)(x+2)
=(x−2)[(x2+2x+4)−(x+2)]=(x−2)(x2+x+2)=(x−2)[(x2+2x+4)−(x+2)]=(x−2)(x2+x+2)
Ví dụ 3: f(x)=3x3–7x2+17x–5f(x)=3x3–7x2+17x–5
Hướng dẫn:
±1,±5±1,±5 không là nghiệm của f(x)f(x), như vậy f(x)f(x) không có nghiệm nguyên. Nên f(x)f(x) nếu có nghiệm thì là nghiệm hữu tỉ
Ta nhận thấy x=x= 1313 là nghiệm của f(x)f(x) do đó f(x)f(x) có một nhân tử là 3x–13x–1. Nên
f(x)=3x3–7x2+17x–5=3x3−x2−6x2+2x+15x−5f(x)=3x3–7x2+17x–5=3x3−x2−6x2+2x+15x−5
=(3x3−x2)−(6x2−2x)+(15x−5)=(3x3−x2)−(6x2−2x)+(15x−5)
= x2(3x−1)−2x(3x−1)+5(3x−1)=(3x−1)(x2−2x+5)x2(3x−1)−2x(3x−1)+5(3x−1)=(3x−1)(x2−2x+5)
Vì x2−2x+5=(x2−2x+1)+4=(x−1)2+4>0x2−2x+5=(x2−2x+1)+4=(x−1)2+4>0 với mọi xx nên không phân tích được thành nhân tử nữa
Ví dụ 4: x3+5x2+8x+4x3+5x2+8x+4
Hướng dẫn:
Tổng các hệ số của các hạng tử bậc chẵn bằng tổng các hệ số của các hạng tử bậc lẻ nên đa thức có một nhân tử là x+1x+1
x3+5x2+8x+4=(x3+x2)+(4x2+4x)+(4x+4)x3+5x2+8x+4=(x3+x2)+(4x2+4x)+(4x+4)
=x2(x+1)+4x(x+1)+4(x+1)=x2(x+1)+4x(x+1)+4(x+1)
=(x+1)(x2+4x+4)=(x+1)(x+2)2=(x+1)(x2+4x+4)=(x+1)(x+2)2
Ví dụ 5: f(x)=x5–2x4+3x3–4x2+2f(x)=x5–2x4+3x3–4x2+2
Hướng dẫn:
Tổng các hệ số bằng 0 thì nên đa thức có một nhân tử là x–1x–1, chia f(x)f(x) cho (x–1)(x–1) ta có:
x5–2x4+3x3–4x2+2=(x–1)(x4−x3+2x2−2x−2)x5–2x4+3x3–4x2+2=(x–1)(x4−x3+2x2−2x−2)
Vì x4−x3+2x2−2x−2x4−x3+2x2−2x−2 không có nghiệm nguyên cũng không có nghiệm hữu tỉ nên không phân tích được nữa
Ví dụ 6: x4+1997x2+1996x+1997x4+1997x2+1996x+1997
Hướng dẫn:
x4+1997x2+1996x+1997=(x4+x2+1)+(1996x2+1996x+1996)x4+1997x2+1996x+1997=(x4+x2+1)+(1996x2+1996x+1996)
=(x2+x+1)(x2−x+1)+1996(x2+x+1)=(x2+x+1)(x2−x+1)+1996(x2+x+1)
=(x2+x+1)(x2−x+1+1996)=(x2+x+1)(x2−x+1997)=(x2+x+1)(x2−x+1+1996)=(x2+x+1)(x2−x+1997)
Ví dụ 7: x2−x−2001.2002x2−x−2001.2002
Hướng dẫn:
x2−x−2001.2002=x2−x−2001.(2001+1)x2−x−2001.2002=x2−x−2001.(2001+1)
=x2−x–20012−2001=(x2–20012)–(x+2001)=(x+2001)(x–2002)=x2−x–20012−2001=(x2–20012)–(x+2001)=(x+2001)(x–2002)
II. THÊM , BỚT CÙNG MỘT HẠNG TỬ:
1. Thêm, bớt cùng một số hạng tử để xuất hiện hiệu hai bình phương:
Ví dụ 1: 4x4+814x4+81
Hướng dẫn:
4x4+81=4x4+36x2+81−36x2=(2x2+9)2–36x24x4+81=4x4+36x2+81−36x2=(2x2+9)2–36x2
=(2x2+9)2–(6x)2=(2x2+9+6x)(2x2+9–6x)=(2x2+9)2–(6x)2=(2x2+9+6x)(2x2+9–6x)
=(2x2+6x+9)(2x2–6x+9)=(2x2+6x+9)(2x2–6x+9)
Ví dụ 2: x8+98x4+1=x8+98x4+1=
Hướng dẫn:
x8+98x4+1=(x8+2x4+1)+96x4x8+98x4+1=(x8+2x4+1)+96x4
=(x4+1)2+16x2(x4+1)+64x4−16x2(x4+1)+32x4=(x4+1)2+16x2(x4+1)+64x4−16x2(x4+1)+32x4
=(x4+1+8x2)2–16x2(x4+1–2x2)=(x4+1+8x2)2–16x2(x4+1–2x2)
=(x4+8x2+1)2−16x2(x2–1)2=(x4+8x2+1)2−16x2(x2–1)2
=(x4+8x2+1)2−(4x3–4x)2=(x4+8x2+1)2−(4x3–4x)2
=(x4+4x3+8x2–4x+1)(x4−4x3+8x2+4x+1)=(x4+4x3+8x2–4x+1)(x4−4x3+8x2+4x+1)
2. Thêm, bớt cùng một số hạng tử để xuất hiện nhân tử chung
Ví dụ 1: x7+x2+1x7+x2+1
Hướng dẫn:
x7+x2+1=(x7–x)+(x2+x+1)x7+x2+1=(x7–x)+(x2+x+1)
=x(x6–1)+(x2+x+1)=x(x6–1)+(x2+x+1)
=x(x3−1)(x3+1)+(x2+x+1)=x(x3−1)(x3+1)+(x2+x+1)
=x(x–1)(x2+x+1)(x3+1)+(x2+x+1)=x(x–1)(x2+x+1)(x3+1)+(x2+x+1)
=(x2+x+1)[x(x–1)(x3+1)+1]=(x2+x+1)[x(x–1)(x3+1)+1]
=(x2+x+1)(x5–x4+x2−x+1)=(x2+x+1)(x5–x4+x2−x+1)
Ví dụ 2: x7+x5+1x7+x5+1
Hướng dẫn:
x7+x5+1=(x7–x)+(x5–x2)+(x2+x+1)x7+x5+1=(x7–x)+(x5–x2)+(x2+x+1)
=x(x3–1)(x3+1)+x2(x3–1)+(x2+x+1)=x(x3–1)(x3+1)+x2(x3–1)+(x2+x+1)
=(x2+x+1)(x–1)(x4+x)+x2(x–1)(x2+x+1)+(x2+x+1)=(x2+x+1)(x–1)(x4+x)+x2(x–1)(x2+x+1)+(x2+x+1)
=(x2+x+1)[(x5–x4+x2–x)+(x3–x2)+1]=(x2+x+1)[(x5–x4+x2–x)+(x3–x2)+1]
=(x2+x+1)(x5–x4+x3–x+1)=(x2+x+1)(x5–x4+x3–x+1)
Ghi nhớ:
Các đa thức có dạng x3m+1+x3n+2+1x3m+1+x3n+2+1 như: x7+x2+1;x7+x5+1;x8+x4+1;x5+x+1;x8+x+1;…x7+x2+1;x7+x5+1;x8+x4+1;x5+x+1;x8+x+1;… đều có nhân tử chung là x2+x+1x2+x+1
III. ĐẶT ẨN PHỤ:
Ví dụ 1: x(x+4)(x+6)(x+10)+128x(x+4)(x+6)(x+10)+128
Hướng dẫn:
x(x+4)(x+6)(x+10)+128=[x(x+10)][(x+4)(x+6)]+128x(x+4)(x+6)(x+10)+128=[x(x+10)][(x+4)(x+6)]+128
=(x2+10x)+(x2+10x+24)+128=(x2+10x)+(x2+10x+24)+128
Đặt x2+10x+12=yx2+10x+12=y, đa thức có dạng:
(y–12)(y+12)+128=y2–144+128(y–12)(y+12)+128=y2–144+128
=y2–16=(y+4)(y–4)=y2–16=(y+4)(y–4)
=(x2+10x+8)(x2+10x+16)=(x2+10x+8)(x2+10x+16)
=(x+2)(x+8)(x2+10x+8)=(x+2)(x+8)(x2+10x+8)
Ví dụ 2: A=x4+6x3+7x2–6x+1A=x4+6x3+7x2–6x+1
Hướng dẫn:
Giả sử x≠0x≠0 ta viết
x4+6x3+7x2–6x+1=x2(x2+6x+7–6x+1x2)x4+6x3+7x2–6x+1=x2(x2+6x+7–6x+1x2)
=x2[(x2+1x2=x2[(x2+1x2)+6(x−)+6(x−1x)+7]1x)+7]
Đặt x−1x=yx−1x=y thì x2+1x2=y2+2x2+1x2=y2+2, do đó
A=x2(y2+2+6y+7)=x2(y+3)2=(xy+3x)2A=x2(y2+2+6y+7)=x2(y+3)2=(xy+3x)2
=[x(x−=[x(x−1x1x)2+3x]2=(x2+3x–1)2)2+3x]2=(x2+3x–1)2
Chú ý: Ví dụ trên có thể giải bằng cách áp dụng hằng đẳng thức như sau:
A=x4+6x3+7x2–6x+1=x4+(6x3–2x2)+(9x2–6x+1)A=x4+6x3+7x2–6x+1=x4+(6x3–2x2)+(9x2–6x+1)
=x4+2x2(3x–1)+(3x–1)2=(x2+3x–1)2=x4+2x2(3x–1)+(3x–1)2=(x2+3x–1)2
Ví dụ 3: A=(x2+y2+z2)(x+y+z)2+(xy+yz+zx)2A=(x2+y2+z2)(x+y+z)2+(xy+yz+zx)2
Hướng dẫn:
A=(x2+y2+z2)(x+y+z)2+(xy+yz+zx)2A=(x2+y2+z2)(x+y+z)2+(xy+yz+zx)2
=[(x2+y2+z2)+2(xy+yz+zx)](x2+y2+z2)+(xy+yz+zx)2=[(x2+y2+z2)+2(xy+yz+zx)](x2+y2+z2)+(xy+yz+zx)2
Đặt x2+y2+z2x2+y2+z2=a,xy+yz+zx=b=a,xy+yz+zx=b ta có
A=a(a+2b)+b2=a2+2ab+b2=(a+b)2A=a(a+2b)+b2=a2+2ab+b2=(a+b)2
=(x2+y2+z2=(x2+y2+z2+xy+yz+zx)2+xy+yz+zx)2
Ví dụ 4: B=2(x4+y4+z4)−(x2+y2+z2)2−2(x2B=2(x4+y4+z4)−(x2+y2+z2)2−2(x2
+y2+z2)(x+y+z)2+(x+y+z)4+y2+z2)(x+y+z)2+(x+y+z)4
Hướng dẫn:
Đặt x4+y2+z2=a,x2+y2+z2=b,x+y+z=cx4+y2+z2=a,x2+y2+z2=b,x+y+z=c ta có:
B=2a–b2–2bc2+c4B=2a–b2–2bc2+c4
=2a–2b2+b2−2bc2+c4=2(a–b2)+(b–c2)2=2a–2b2+b2−2bc2+c4=2(a–b2)+(b–c2)2
Ta lại có: a–b2=−2(x2y2+y2z2+z2x2a–b2=−2(x2y2+y2z2+z2x2) và b–c2=−2(xy+yz+zx)b–c2=−2(xy+yz+zx) Do đó:
B=−4(x2y2+y2z2+z2x2)+4(xy+yz+zx)2B=−4(x2y2+y2z2+z2x2)+4(xy+yz+zx)2
=−4x2y2−4y2z2−4z2x2+4x2y2+4y2z2+4z2x2+8x2yz+8xy2z+8xyz2=−4x2y2−4y2z2−4z2x2+4x2y2+4y2z2+4z2x2+8x2yz+8xy2z+8xyz2
=8xyz(x+y+z)=8xyz(x+y+z)
Ví dụ 5: (a+b+c)3−4(a3+b3+c3)−12abc(a+b+c)3−4(a3+b3+c3)−12abc
Đặt a+b=m,a–b=na+b=m,a–b=n thì 4ab=m2–n24ab=m2–n2
a3+b3=(a+b)[(a–b)2+ab]=m(n2+a3+b3=(a+b)[(a–b)2+ab]=m(n2+m2−n24m2−n24).
Ta có:
C=(m+c)3–4.C=(m+c)3–4.m3+3mn24−4c3−3c(m2−n2)m3+3mn24−4c3−3c(m2−n2)
=3(−c3+mc2–mn2+cn2)=3(−c3+mc2–mn2+cn2)
=3[c2(m−c)−n2(m−c)]=3(m−c)(c−n)(c+n)=3[c2(m−c)−n2(m−c)]=3(m−c)(c−n)(c+n)
=3(a+b−c)(c+a−b)(c−a+b)=3(a+b−c)(c+a−b)(c−a+b)
IV. PHƯƠNG PHÁP HỆ SỐ BẤT ĐỊNH:
Ví dụ 1: x4−6x3+12x2−14x+3x4−6x3+12x2−14x+3
Hướng dẫn:
Các số ±±1, ±±3 không là nghiệm của đa thức, đa thức không có nghiệm nguyên củng không có nghiệm hữu tỉ.
Như vậy nếu đa thức phân tích được thành nhân tử thì phải có dạng
(x2+ax+b)(x2+cx+d)=x4+(a+c)x3+(ac+b+d)x2+(ad+bc)x+bd(x2+ax+b)(x2+cx+d)=x4+(a+c)x3+(ac+b+d)x2+(ad+bc)x+bd
đồng nhất đa thức này với đa thức đã cho ta có:
⎧⎩⎨⎪⎪⎪⎪⎪⎪+c=−6ac+b+d=12ad+bc=−14bd=3{+c=−6ac+b+d=12ad+bc=−14bd=3
Xét bd=3bd=3 với b,d∈Z,b∈{±1,±3}b,d∈Z,b∈{±1,±3}
Với b=3b=3 thì d=1d=1 hệ điều kiện trên trở thành:
⎧⎩⎨⎪⎪⎪⎪⎪⎪+c=−6ac=−8a+3c=−14bd=3⇒{c=−8ac=8⇒{=−4a=−2{+c=−6ac=−8a+3c=−14bd=3⇒{c=−8ac=8⇒{=−4a=−2
Vậy: x4−6x3+12x2−14x+3=(x2−2x+3)(x2−4x+1)x4−6x3+12x2−14x+3=(x2−2x+3)(x2−4x+1)
Ví dụ 2: 2x4−3x3−7x2+6x+82x4−3x3−7x2+6x+8
Hướng dẫn:
Đa thức có 1 nghiệm là x=2x=2 nên có thừa số là x–2x–2 do đó ta có:
2x4−3x3−7x2+6x+8=(x−2)(2x3+ax2+bx+c)2x4−3x3−7x2+6x+8=(x−2)(2x3+ax2+bx+c)
=2x4+(a−4)x3+(b−2a)x2+(c−2b)x−2c=2x4+(a−4)x3+(b−2a)x2+(c−2b)x−2c
⇒⇒ ⎧⎩⎨⎪⎪⎪⎪⎪⎪−4=−3b−2a=−7c−2b=6−2c=8⇒⎧⎩⎨⎪⎪=1b=−5c=−4{−4=−3b−2a=−7c−2b=6−2c=8⇒{=1b=−5c=−4
Suy ra: 2x4−3x3−7x2+6x+8=(x−2)(2x3+x2−5x−4)2x4−3x3−7x2+6x+8=(x−2)(2x3+x2−5x−4)
Ta lại có 2x3+x2−5x−42x3+x2−5x−4 là đa thức có tổng hệ số của các hạng tử bậc lẻ và bậc chẵn bằng nhau nên có 1 nhân tử là x+1x+1
Nên 2x3+x2−5x−4=(x+1)(2x2−x−4)2x3+x2−5x−4=(x+1)(2x2−x−4)
Vậy: 2x4−3x3−7x2+6x+8=(x−2)(x+1)(2x2−x−4)2x4−3x3−7x2+6x+8=(x−2)(x+1)(2x2−x−4)
Ví dụ 3: 12x2+5x−12y2+12y−10xy−312x2+5x−12y2+12y−10xy−3
Hướng dẫn:
12x2+5x−12y2+12y−10xy−3=(ax+by+3)(cx+dy−1)12x2+5x−12y2+12y−10xy−3=(ax+by+3)(cx+dy−1)
=acx2+(3c−a)x+bdy2+(3d−b)y+(bc+ad)xy–3=acx2+(3c−a)x+bdy2+(3d−b)y+(bc+ad)xy–3
⇒⇒⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪c=12bc+ad=−103c−a=5bd=−123d−b=12⇒⎧⎩⎨⎪⎪⎪⎪⎪⎪=4c=3b=−6d=2{c=12bc+ad=−103c−a=5bd=−123d−b=12⇒{=4c=3b=−6d=2
⇒⇒ 12x2+5x−12y2+12y−10xy−3=(4x−6y+3)(3x+2y−1)
Phân tích đa thức thành nhân tử có 3 phương pháp:
- Phương pháp đặt nhân tử chung
- Phương pháp dùng hẳng thức
- Phương pháp nhóm hạng tử
Phân tích đa thức thành nhân tử có 3 phương pháp:
- Phương pháp đặt nhân tử chung
- Phương pháp dùng hẳng thức
- Phương pháp nhóm hạng tử
Phân tích đa thức thành nhân tử có 3 phương pháp:
- Phương pháp đặt nhân tử chung
- Phương pháp dùng hẳng thức
- Phương pháp nhóm hạng tử
Phân tích đa thức thành nhân tử có 3 phương pháp:
- Phương pháp đặt nhân tử chung
- Phương pháp dùng hẳng thức
- Phương pháp nhóm hạng tử
Phân tích đa thức thành nhân tử có 3 phương pháp:
- Phương pháp đặt nhân tử chung
- Phương pháp dùng hẳng thức
- Phương pháp nhóm hạng tử
Phân tích đa thức thành nhân tử có 3 phương pháp:
- Phương pháp đặt nhân tử chung
- Phương pháp dùng hẳng thức
- Phương pháp nhóm hạng tử
Phân tích đa thức thành nhân tử có 3 phương pháp:
- Phương pháp đặt nhân tử chung
- Phương pháp dùng hẳng thức
- Phương pháp nhóm hạng tử
Ta sẽ tìm hiểu về các phương pháp sau:
1. Tách một hạng tử thành nhiều hạng tử
2. Thêm, bớt cùng một hạng tử
3. Đặt ẩn phụ
4. Phương pháp hệ số bất định
I. TÁCH MỘT HẠNG TỬ THÀNH NHIỀU HẠNG TỬ:
Định lí bổ sung:
+ Đa thức f(x)f(x) có nghiệm hữu tỉ thì có dạng pqpq trong đó pp là ước của hệ số tự do, qq là ước dương của hệ số cao nhất
+ Nếu f(x)f(x) có tổng các hệ số bằng 0 thì f(x)f(x) có một nhân tử là x–1x–1
+ Nếu f(x)f(x) có tổng các hệ số của các hạng tử bậc chẵn bằng tổng các hệ số của các hạng tử bậc lẻ thì f(x)f(x) có một nhân tử là x+1x+1
+ Nếu aa là nghiệm nguyên của f(x)f(x) và f(1);f(−1)f(1);f(−1) khác 0 thì f(1)a−1f(1)a−1 và f(−1)a+1f(−1)a+1 đều là số nguyên. Để nhanh chóng loại trừ nghiệm là ước của hệ số tự do
Ví dụ 1: 3x2–8x+43x2–8x+4
Hướng dẫn:
Cách 1: Tách hạng tử thứ 2
3x2–8x+4=3x2–6x–2x+4=3x(x–2)–2(x–2)=(x–2)(3x–2)3x2–8x+4=3x2–6x–2x+4=3x(x–2)–2(x–2)=(x–2)(3x–2)
Cách 2: Tách hạng tử thứ nhất:
3x2–8x+4=(4x2–8x+4)−x2=(2x–2)2–x2=(2x–2+x)(2x–2–x)3x2–8x+4=(4x2–8x+4)−x2=(2x–2)2–x2=(2x–2+x)(2x–2–x)
=(x–2)(3x–2)=(x–2)(3x–2)
Ví dụ 2: x3–x2–4x3–x2–4
Hướng dẫn:
Ta nhận thấy nghiệm của f(x)f(x) nếu có thì x = ±1;±2;±4±1;±2;±4, chỉ có f(2)=0f(2)=0 nên x=2x=2 là nghiệm của f(x)f(x) nên f(x)f(x) có một nhân tử là x–2x–2. Do đó ta tách f(x)f(x) thành các nhóm có xuất hiện một nhân tử là x–2x–2
Cách 1:
x3–x2–4=x3–x2–4= (x3−2x2)+(x2−2x)+(2x−4)(x3−2x2)+(x2−2x)+(2x−4)
=x2(x−2)+x(x−2)+2(x−2)=(x−2)(x2+x+2)=x2(x−2)+x(x−2)+2(x−2)=(x−2)(x2+x+2)
Cách 2:
x3−x2−4=x3−8−x2+4x3−x2−4=x3−8−x2+4
=(x3−8)−(x2−4)=(x−2)(x2+2x+4)−(x−2)(x+2)=(x3−8)−(x2−4)=(x−2)(x2+2x+4)−(x−2)(x+2)
=(x−2)[(x2+2x+4)−(x+2)]=(x−2)(x2+x+2)=(x−2)[(x2+2x+4)−(x+2)]=(x−2)(x2+x+2)
Ví dụ 3: f(x)=3x3–7x2+17x–5f(x)=3x3–7x2+17x–5
Hướng dẫn:
±1,±5±1,±5 không là nghiệm của f(x)f(x), như vậy f(x)f(x) không có nghiệm nguyên. Nên f(x)f(x) nếu có nghiệm thì là nghiệm hữu tỉ
Ta nhận thấy x=x= 1313 là nghiệm của f(x)f(x) do đó f(x)f(x) có một nhân tử là 3x–13x–1. Nên
f(x)=3x3–7x2+17x–5=3x3−x2−6x2+2x+15x−5f(x)=3x3–7x2+17x–5=3x3−x2−6x2+2x+15x−5
=(3x3−x2)−(6x2−2x)+(15x−5)=(3x3−x2)−(6x2−2x)+(15x−5)
= x2(3x−1)−2x(3x−1)+5(3x−1)=(3x−1)(x2−2x+5)x2(3x−1)−2x(3x−1)+5(3x−1)=(3x−1)(x2−2x+5)
Vì x2−2x+5=(x2−2x+1)+4=(x−1)2+4>0x2−2x+5=(x2−2x+1)+4=(x−1)2+4>0 với mọi xx nên không phân tích được thành nhân tử nữa
Ví dụ 4: x3+5x2+8x+4x3+5x2+8x+4
Hướng dẫn:
Tổng các hệ số của các hạng tử bậc chẵn bằng tổng các hệ số của các hạng tử bậc lẻ nên đa thức có một nhân tử là x+1x+1
x3+5x2+8x+4=(x3+x2)+(4x2+4x)+(4x+4)x3+5x2+8x+4=(x3+x2)+(4x2+4x)+(4x+4)
=x2(x+1)+4x(x+1)+4(x+1)=x2(x+1)+4x(x+1)+4(x+1)
=(x+1)(x2+4x+4)=(x+1)(x+2)2=(x+1)(x2+4x+4)=(x+1)(x+2)2
Ví dụ 5: f(x)=x5–2x4+3x3–4x2+2f(x)=x5–2x4+3x3–4x2+2
Hướng dẫn:
Tổng các hệ số bằng 0 thì nên đa thức có một nhân tử là x–1x–1, chia f(x)f(x) cho (x–1)(x–1) ta có:
x5–2x4+3x3–4x2+2=(x–1)(x4−x3+2x2−2x−2)x5–2x4+3x3–4x2+2=(x–1)(x4−x3+2x2−2x−2)
Vì x4−x3+2x2−2x−2x4−x3+2x2−2x−2 không có nghiệm nguyên cũng không có nghiệm hữu tỉ nên không phân tích được nữa
Ví dụ 6: x4+1997x2+1996x+1997x4+1997x2+1996x+1997
Hướng dẫn:
x4+1997x2+1996x+1997=(x4+x2+1)+(1996x2+1996x+1996)x4+1997x2+1996x+1997=(x4+x2+1)+(1996x2+1996x+1996)
=(x2+x+1)(x2−x+1)+1996(x2+x+1)=(x2+x+1)(x2−x+1)+1996(x2+x+1)
=(x2+x+1)(x2−x+1+1996)=(x2+x+1)(x2−x+1997)=(x2+x+1)(x2−x+1+1996)=(x2+x+1)(x2−x+1997)
Ví dụ 7: x2−x−2001.2002x2−x−2001.2002
Hướng dẫn:
x2−x−2001.2002=x2−x−2001.(2001+1)x2−x−2001.2002=x2−x−2001.(2001+1)
=x2−x–20012−2001=(x2–20012)–(x+2001)=(x+2001)(x–2002)=x2−x–20012−2001=(x2–20012)–(x+2001)=(x+2001)(x–2002)
II. THÊM , BỚT CÙNG MỘT HẠNG TỬ:
1. Thêm, bớt cùng một số hạng tử để xuất hiện hiệu hai bình phương:
Ví dụ 1: 4x4+814x4+81
Hướng dẫn:
4x4+81=4x4+36x2+81−36x2=(2x2+9)2–36x24x4+81=4x4+36x2+81−36x2=(2x2+9)2–36x2
=(2x2+9)2–(6x)2=(2x2+9+6x)(2x2+9–6x)=(2x2+9)2–(6x)2=(2x2+9+6x)(2x2+9–6x)
=(2x2+6x+9)(2x2–6x+9)=(2x2+6x+9)(2x2–6x+9)
Ví dụ 2: x8+98x4+1=x8+98x4+1=
Hướng dẫn:
x8+98x4+1=(x8+2x4+1)+96x4x8+98x4+1=(x8+2x4+1)+96x4
=(x4+1)2+16x2(x4+1)+64x4−16x2(x4+1)+32x4=(x4+1)2+16x2(x4+1)+64x4−16x2(x4+1)+32x4
=(x4+1+8x2)2–16x2(x4+1–2x2)=(x4+1+8x2)2–16x2(x4+1–2x2)
=(x4+8x2+1)2−16x2(x2–1)2=(x4+8x2+1)2−16x2(x2–1)2
=(x4+8x2+1)2−(4x3–4x)2=(x4+8x2+1)2−(4x3–4x)2
=(x4+4x3+8x2–4x+1)(x4−4x3+8x2+4x+1)=(x4+4x3+8x2–4x+1)(x4−4x3+8x2+4x+1)
2. Thêm, bớt cùng một số hạng tử để xuất hiện nhân tử chung
Ví dụ 1: x7+x2+1x7+x2+1
Hướng dẫn:
x7+x2+1=(x7–x)+(x2+x+1)x7+x2+1=(x7–x)+(x2+x+1)
=x(x6–1)+(x2+x+1)=x(x6–1)+(x2+x+1)
=x(x3−1)(x3+1)+(x2+x+1)=x(x3−1)(x3+1)+(x2+x+1)
=x(x–1)(x2+x+1)(x3+1)+(x2+x+1)=x(x–1)(x2+x+1)(x3+1)+(x2+x+1)
=(x2+x+1)[x(x–1)(x3+1)+1]=(x2+x+1)[x(x–1)(x3+1)+1]
=(x2+x+1)(x5–x4+x2−x+1)=(x2+x+1)(x5–x4+x2−x+1)
Ví dụ 2: x7+x5+1x7+x5+1
Hướng dẫn:
x7+x5+1=(x7–x)+(x5–x2)+(x2+x+1)x7+x5+1=(x7–x)+(x5–x2)+(x2+x+1)
=x(x3–1)(x3+1)+x2(x3–1)+(x2+x+1)=x(x3–1)(x3+1)+x2(x3–1)+(x2+x+1)
=(x2+x+1)(x–1)(x4+x)+x2(x–1)(x2+x+1)+(x2+x+1)=(x2+x+1)(x–1)(x4+x)+x2(x–1)(x2+x+1)+(x2+x+1)
=(x2+x+1)[(x5–x4+x2–x)+(x3–x2)+1]=(x2+x+1)[(x5–x4+x2–x)+(x3–x2)+1]
=(x2+x+1)(x5–x4+x3–x+1)=(x2+x+1)(x5–x4+x3–x+1)
Ghi nhớ:
Các đa thức có dạng x3m+1+x3n+2+1x3m+1+x3n+2+1 như: x7+x2+1;x7+x5+1;x8+x4+1;x5+x+1;x8+x+1;…x7+x2+1;x7+x5+1;x8+x4+1;x5+x+1;x8+x+1;… đều có nhân tử chung là x2+x+1x2+x+1
III. ĐẶT ẨN PHỤ:
Ví dụ 1: x(x+4)(x+6)(x+10)+128x(x+4)(x+6)(x+10)+128
Hướng dẫn:
x(x+4)(x+6)(x+10)+128=[x(x+10)][(x+4)(x+6)]+128x(x+4)(x+6)(x+10)+128=[x(x+10)][(x+4)(x+6)]+128
=(x2+10x)+(x2+10x+24)+128=(x2+10x)+(x2+10x+24)+128
Đặt x2+10x+12=yx2+10x+12=y, đa thức có dạng:
(y–12)(y+12)+128=y2–144+128(y–12)(y+12)+128=y2–144+128
=y2–16=(y+4)(y–4)=y2–16=(y+4)(y–4)
=(x2+10x+8)(x2+10x+16)=(x2+10x+8)(x2+10x+16)
=(x+2)(x+8)(x2+10x+8)=(x+2)(x+8)(x2+10x+8)
Ví dụ 2: A=x4+6x3+7x2–6x+1A=x4+6x3+7x2–6x+1
Hướng dẫn:
Giả sử x≠0x≠0 ta viết
x4+6x3+7x2–6x+1=x2(x2+6x+7–6x+1x2)x4+6x3+7x2–6x+1=x2(x2+6x+7–6x+1x2)
=x2[(x2+1x2=x2[(x2+1x2)+6(x−)+6(x−1x)+7]1x)+7]
Đặt x−1x=yx−1x=y thì x2+1x2=y2+2x2+1x2=y2+2, do đó
A=x2(y2+2+6y+7)=x2(y+3)2=(xy+3x)2A=x2(y2+2+6y+7)=x2(y+3)2=(xy+3x)2
=[x(x−=[x(x−1x1x)2+3x]2=(x2+3x–1)2)2+3x]2=(x2+3x–1)2
Chú ý: Ví dụ trên có thể giải bằng cách áp dụng hằng đẳng thức như sau:
A=x4+6x3+7x2–6x+1=x4+(6x3–2x2)+(9x2–6x+1)A=x4+6x3+7x2–6x+1=x4+(6x3–2x2)+(9x2–6x+1)
=x4+2x2(3x–1)+(3x–1)2=(x2+3x–1)2=x4+2x2(3x–1)+(3x–1)2=(x2+3x–1)2
Ví dụ 3: A=(x2+y2+z2)(x+y+z)2+(xy+yz+zx)2A=(x2+y2+z2)(x+y+z)2+(xy+yz+zx)2
Hướng dẫn:
A=(x2+y2+z2)(x+y+z)2+(xy+yz+zx)2A=(x2+y2+z2)(x+y+z)2+(xy+yz+zx)2
=[(x2+y2+z2)+2(xy+yz+zx)](x2+y2+z2)+(xy+yz+zx)2=[(x2+y2+z2)+2(xy+yz+zx)](x2+y2+z2)+(xy+yz+zx)2
Đặt x2+y2+z2x2+y2+z2=a,xy+yz+zx=b=a,xy+yz+zx=b ta có
A=a(a+2b)+b2=a2+2ab+b2=(a+b)2A=a(a+2b)+b2=a2+2ab+b2=(a+b)2
=(x2+y2+z2=(x2+y2+z2+xy+yz+zx)2+xy+yz+zx)2
Ví dụ 4: B=2(x4+y4+z4)−(x2+y2+z2)2−2(x2B=2(x4+y4+z4)−(x2+y2+z2)2−2(x2
+y2+z2)(x+y+z)2+(x+y+z)4+y2+z2)(x+y+z)2+(x+y+z)4
Hướng dẫn:
Đặt x4+y2+z2=a,x2+y2+z2=b,x+y+z=cx4+y2+z2=a,x2+y2+z2=b,x+y+z=c ta có:
B=2a–b2–2bc2+c4B=2a–b2–2bc2+c4
=2a–2b2+b2−2bc2+c4=2(a–b2)+(b–c2)2=2a–2b2+b2−2bc2+c4=2(a–b2)+(b–c2)2
Ta lại có: a–b2=−2(x2y2+y2z2+z2x2a–b2=−2(x2y2+y2z2+z2x2) và b–c2=−2(xy+yz+zx)b–c2=−2(xy+yz+zx) Do đó:
B=−4(x2y2+y2z2+z2x2)+4(xy+yz+zx)2B=−4(x2y2+y2z2+z2x2)+4(xy+yz+zx)2
=−4x2y2−4y2z2−4z2x2+4x2y2+4y2z2+4z2x2+8x2yz+8xy2z+8xyz2=−4x2y2−4y2z2−4z2x2+4x2y2+4y2z2+4z2x2+8x2yz+8xy2z+8xyz2
=8xyz(x+y+z)=8xyz(x+y+z)
Ví dụ 5: (a+b+c)3−4(a3+b3+c3)−12abc(a+b+c)3−4(a3+b3+c3)−12abc
Đặt a+b=m,a–b=na+b=m,a–b=n thì 4ab=m2–n24ab=m2–n2
a3+b3=(a+b)[(a–b)2+ab]=m(n2+a3+b3=(a+b)[(a–b)2+ab]=m(n2+m2−n24m2−n24).
Ta có:
C=(m+c)3–4.C=(m+c)3–4.m3+3mn24−4c3−3c(m2−n2)m3+3mn24−4c3−3c(m2−n2)
=3(−c3+mc2–mn2+cn2)=3(−c3+mc2–mn2+cn2)
=3[c2(m−c)−n2(m−c)]=3(m−c)(c−n)(c+n)=3[c2(m−c)−n2(m−c)]=3(m−c)(c−n)(c+n)
=3(a+b−c)(c+a−b)(c−a+b)=3(a+b−c)(c+a−b)(c−a+b)
IV. PHƯƠNG PHÁP HỆ SỐ BẤT ĐỊNH:
Ví dụ 1: x4−6x3+12x2−14x+3x4−6x3+12x2−14x+3
Hướng dẫn:
Các số ±±1, ±±3 không là nghiệm của đa thức, đa thức không có nghiệm nguyên củng không có nghiệm hữu tỉ.
Như vậy nếu đa thức phân tích được thành nhân tử thì phải có dạng
(x2+ax+b)(x2+cx+d)=x4+(a+c)x3+(ac+b+d)x2+(ad+bc)x+bd(x2+ax+b)(x2+cx+d)=x4+(a+c)x3+(ac+b+d)x2+(ad+bc)x+bd
đồng nhất đa thức này với đa thức đã cho ta có:
⎧⎩⎨⎪⎪⎪⎪⎪⎪+c=−6ac+b+d=12ad+bc=−14bd=3{+c=−6ac+b+d=12ad+bc=−14bd=3
Xét bd=3bd=3 với b,d∈Z,b∈{±1,±3}b,d∈Z,b∈{±1,±3}
Với b=3b=3 thì d=1d=1 hệ điều kiện trên trở thành:
⎧⎩⎨⎪⎪⎪⎪⎪⎪+c=−6ac=−8a+3c=−14bd=3⇒{c=−8ac=8⇒{=−4a=−2{+c=−6ac=−8a+3c=−14bd=3⇒{c=−8ac=8⇒{=−4a=−2
Vậy: x4−6x3+12x2−14x+3=(x2−2x+3)(x2−4x+1)x4−6x3+12x2−14x+3=(x2−2x+3)(x2−4x+1)
Ví dụ 2: 2x4−3x3−7x2+6x+82x4−3x3−7x2+6x+8
Hướng dẫn:
Đa thức có 1 nghiệm là x=2x=2 nên có thừa số là x–2x–2 do đó ta có:
2x4−3x3−7x2+6x+8=(x−2)(2x3+ax2+bx+c)2x4−3x3−7x2+6x+8=(x−2)(2x3+ax2+bx+c)
=2x4+(a−4)x3+(b−2a)x2+(c−2b)x−2c=2x4+(a−4)x3+(b−2a)x2+(c−2b)x−2c
⇒⇒ ⎧⎩⎨⎪⎪⎪⎪⎪⎪−4=−3b−2a=−7c−2b=6−2c=8⇒⎧⎩⎨⎪⎪=1b=−5c=−4{−4=−3b−2a=−7c−2b=6−2c=8⇒{=1b=−5c=−4
Suy ra: 2x4−3x3−7x2+6x+8=(x−2)(2x3+x2−5x−4)2x4−3x3−7x2+6x+8=(x−2)(2x3+x2−5x−4)
Ta lại có 2x3+x2−5x−42x3+x2−5x−4 là đa thức có tổng hệ số của các hạng tử bậc lẻ và bậc chẵn bằng nhau nên có 1 nhân tử là x+1x+1
Nên 2x3+x2−5x−4=(x+1)(2x2−x−4)2x3+x2−5x−4=(x+1)(2x2−x−4)
Vậy: 2x4−3x3−7x2+6x+8=(x−2)(x+1)(2x2−x−4)2x4−3x3−7x2+6x+8=(x−2)(x+1)(2x2−x−4)
Ví dụ 3: 12x2+5x−12y2+12y−10xy−312x2+5x−12y2+12y−10xy−3
Hướng dẫn:
12x2+5x−12y2+12y−10xy−3=(ax+by+3)(cx+dy−1)12x2+5x−12y2+12y−10xy−3=(ax+by+3)(cx+dy−1)
=acx2+(3c−a)x+bdy2+(3d−b)y+(bc+ad)xy–3=acx2+(3c−a)x+bdy2+(3d−b)y+(bc+ad)xy–3
⇒⇒⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪c=12bc+ad=−103c−a=5bd=−123d−b=12⇒⎧⎩⎨⎪⎪⎪⎪⎪⎪=4c=3b=−6d=2{c=12bc+ad=−103c−a=5bd=−123d−b=12⇒{=4c=3b=−6d=2
⇒⇒ 12x2+5x−12y2+12y−10xy−3=(4x−6y+3)(3x+2y−1)12x2+5x−12y2+12y−10xy−3=(4x−6y+3)(3x+2y−1)
phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hangj tử(kè công thức dùm )
phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hạng tử)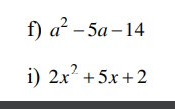
phân tích đa thức sau thành nhân tử(tách 1 hạng tử 
