\(=x\left(x^2-2x+1-y^2\right)=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-1-y\right)\left(x-1+y\right)\)
cách phân tích đa thức có dạng ax + b\(\sqrt{x}\) + c thành nhân tử với x > 0
từ đó phân tích đa thức x +8 \(\sqrt{x}\) + 7 thành nhân tử với x > 0
Phân tích đa thức thành nhân tử
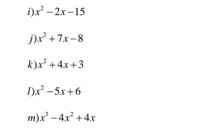
phân tích đa thức thành nhân tử vs ạ
Phân tích đa thức thành nhân tử x*\(\sqrt{x}\) +1
phân tích đa thức thành nhân tử
\(x-5\sqrt{x}+6\)
phân tích đa thức thành nhân tử \(\text{x^2-6x+7}\)
\(5\sqrt{14}-\sqrt[]{21}\)
Phân tích đa thức thành nhân tử
Phân tích đa thức thành nhân tử: x4 - 2x2 - 38x - 122 =0
phân tích đa thức thành nhân tử
\(x-6\sqrt{x}+8\)
