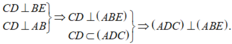Các câu hỏi tương tự
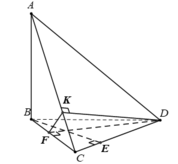
Cho tứ diện ABCD có AB⊥(BCD). Trong ΔBCD vẽ các đường cao BE và DF cắt nhau ở O. Trong mp(ADC), vẽ DK⊥AC tại K. Chứng minh: (ADC)⊥(ABE)
Cho tứ diện ABCD có AB⊥(BCD) . Trong ΔBCD vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ DK⊥AC tại K. Chứng minh: (ADC)⊥(DFK)
Cho tứ diện ABCD có AB⊥(BCD). Trong ΔBCD vẽ các đường cao BE và DF cắt nhau ở O. Trong mp(ADC), vẽ DK⊥AC tại K. Chứng minh: (ADC)⊥(DFK)
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (BCD). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh (ABE)⊥(ADC)
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (BCD). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh (ABC)⊥(DFK)
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (BCD). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh (DFK)⊥(ACD)
Cho tứ diện ABCD có hai mặt ABC và ADC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác ABC vuông tại A có AB =a, AC =b. Tam giác ACD vuông tại D có CD = a.
a) Chứng minh các tam giác BAD và BDC là các tam giác vuông.
b) Gọi I và K lần lượt là trung điểm của AD và BC. Chứng minh IK là đường vuông góc chung của hai đường thẳng AD và BC.
Cho tứ diện ABCD và điểm M nằm trong tam giác BCD.a) Dựng đường thẳng qua M song song với hai mặt phẳng (ABC) và (ABD). Giả sử đường thẳng này cắt mặt phẳng (ACD) tại B.Chứng minh rằng AB, BM và CD đồng quy tại một điểm.b) Chứng minh
M
B
B
A
d
t
∆
M...
Đọc tiếp
Cho tứ diện ABCD và điểm M nằm trong tam giác BCD.
a) Dựng đường thẳng qua M song song với hai mặt phẳng (ABC) và (ABD). Giả sử đường thẳng này cắt mặt phẳng (ACD) tại B'.
Chứng minh rằng AB', BM và CD đồng quy tại một điểm.
b) Chứng minh M B ' B A = d t ∆ M C D d t ∆ B C D
c) Đường thẳng song song với hai mặt phẳng (ACB) và (ACD) kẻ từ M cắt (ABD) tại C' và đường thẳng song song với hai mặt phẳng (ADC) và (ADB) kẻ từ M cắt (ABC) tại D'. Chứng minh rằng M B ' B A + M C ' C A + M D ' D A = 1
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau? A.
A
B
E
⊥
A
D
C
B.
A
B
D
⊥
A...
Đọc tiếp
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chọn khẳng định sai trong các khẳng định sau?
A. A B E ⊥ A D C
B. A B D ⊥ A D C
C. A B C ⊥ D F K
D. D F K ⊥ A D C