Question

Nhanh vote nha

Answer 1

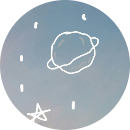
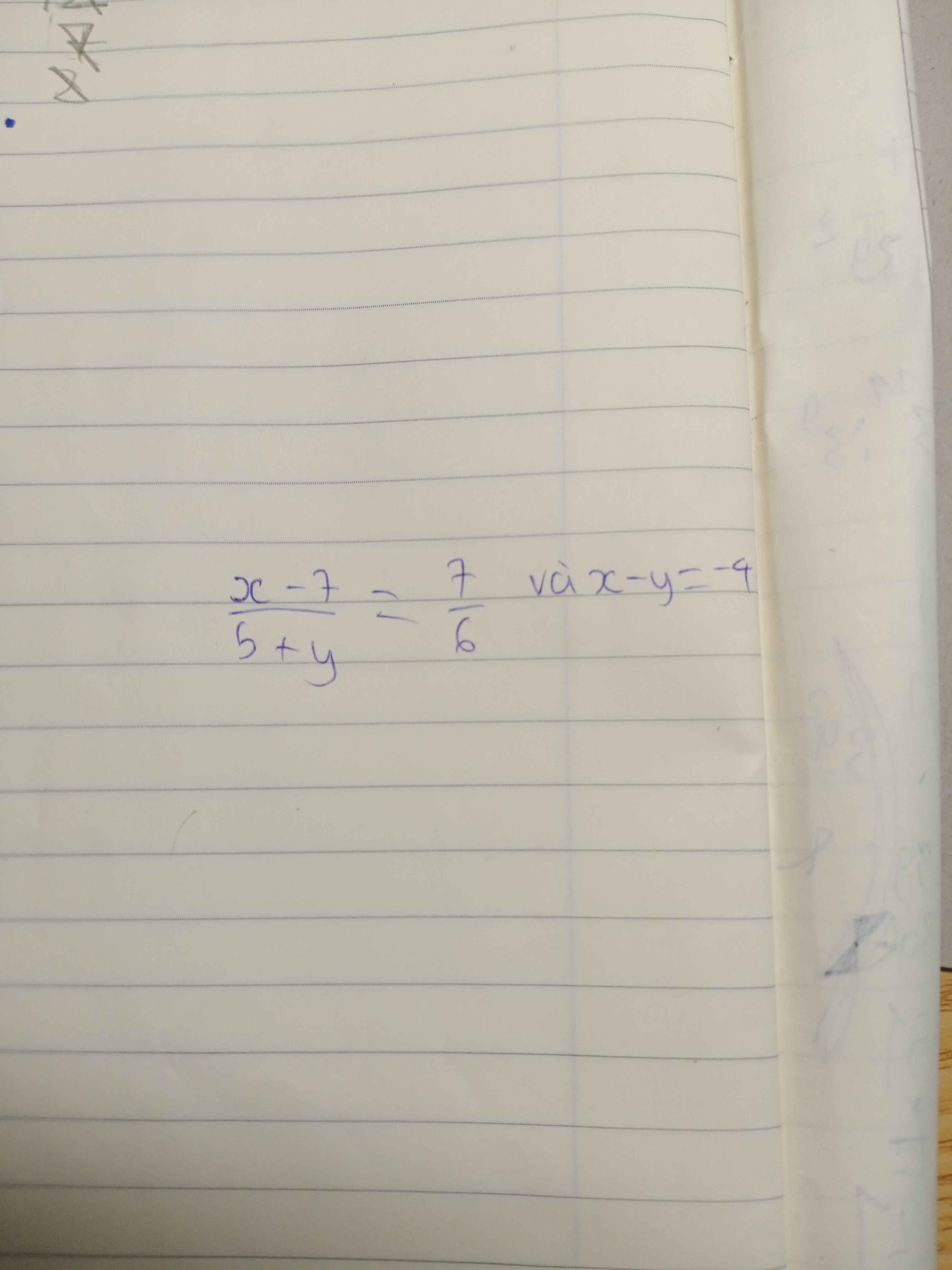\(\left(x+1\right)+\left(x+2\right)+\left(x+3\right)+...+\left(x+100\right)=5150\)

\(100x+\dfrac{\left(100+1\right)\times100}{2}=5150\)

\(100x+5050=5150\)

\(100x=100\)

\(x=1\)

Answer 2

\(\left(x+1\right)+\left(x+2\right)+\left(x+3\right)+...+\left(x+100\right)=5150\)

\(\left(x+x+x+...+x\right)+\left(1+2+3+...+100\right)=5150\)

\(100x+\left(100+1\right).100:2=5150\)

\(100x+5050=5150\)

\(100x=100\)

\(x=1\)

Answer 3

em chụp ngang ra chứ chụp dọc khó đọc lắm em !

Answer 4

(x+1)+(x+2)+(x+3)+(x+4)+...+(x+100) = 5150 
100x + (1 + 2 + 3 + 4 + ... + 100) = 5150 
100x + 5050 = 5150 
100x = 100 
x = 100 : 100 
x = 1 

Answer 5

( 1 + x ) + ( 2 + x ) + ( 3 + x ) + ... + ( x + 100) = 5150

x.100 + 5050 = 5150

x100 = 5150 - 5050

x100 = 100

x = 100 : 100

x = 1