Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Hãy nhắc lại định nghĩa giá trị lượng giác của một góc α với 0o ≤ α ≤ 180o. Tại sao khi α là các góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?
Cho cosα=\(\dfrac{1}{3}\) với 0<α<\(\dfrac{\pi}{2}\).Tính các giá trị lượng giác còn lại của góc α.
Tính các giá trị lượng giác của góc α nếu
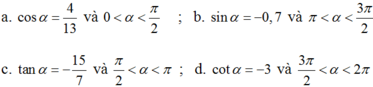
Tính các giá trị lượng giác của góc α, biết
cotα = 4tanα khi π/2 < α < π
Tính các giá trị lượng giác của góc α, biết
cosα = 2sinα khi 0 < α < π/2
Tính các giá trị lượng giác của cung α biết
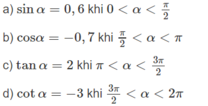
Tam giác ABC vuông tại A có góc nhọn (ABC) ̂ = α. Hãy nhắc lại định nghĩa các tỉ số lượng giác của góc nhọn α đã học ở lớp 9.
Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau cot(α + π)
Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau tan(3π/2 - α)




