Các câu hỏi tương tự
Cho hàm số y f(x) xác định trên tập số thực và có đạo hàm f(x). Đồ thị hàm số y f(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) f(4). - f(3). Giá trị nhỏ nhất của hàm số y f(x) trên đoạn [0;4] là A. f(1) B. f(0) C. f(2) D. f(4)
Đọc tiếp
Cho hàm số y = f(x) xác định trên tập số thực và có đạo hàm f'(x). Đồ thị hàm số y = f'(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) = f(4). - f(3). Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [0;4] là
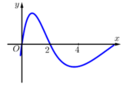
A. f(1)
B. f(0)
C. f(2)
D. f(4)
Cho hai số thực a, b tùy ý, F(x) là một nguyên hàm của hàm số f(x) trên tập
ℝ
. Mệnh đề nào dưới đây là đúng?
Đọc tiếp
Cho hai số thực a, b tùy ý, F(x) là một nguyên hàm của hàm số f(x) trên tập ℝ . Mệnh đề nào dưới đây là đúng?
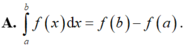
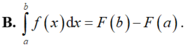
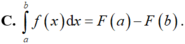
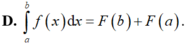
Cho hàm số f(x)3sinx +3. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số
y
f
3
(
x
)
-
3
m
f
2
(
x
)
+
3
(
m
2
-
4
)
f
(
x
)
-
m
nghịch biến trên khoảng
(
0
;...
Đọc tiếp
Cho hàm số f(x)=3sinx +3. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 m f 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng ( 0 ; π 2 ) . Số tập con của S bằng
![]()
![]()
![]()
![]()
Cho hàm số yf(x) có đạo hàm f(x)
(
x
2
-
1
)
(
x
-
2
)
. Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số
f
(
x
2
+
m
)
có 5 điểm cực trị. Số phần tử của tập S là. A. 4 B. 1 C. 3 D. 2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
Cho hàm số y f(x) có đạo hàm f(x). Hàm số y f(x) liên tục trên tập số thực và có bảng biến thiên như sau: Biết rằng f(-1)
10
3
, f(2) 6. Giá trị nhỏ nhất của hàm số g(x)
f
3
(
x
)
-
3
f
(
x
)
trên đoạn [-1;2] bằng A.
10
3
B.
820
27...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f'(x). Hàm số y = f'(x) liên tục trên tập số thực và có bảng biến thiên như sau:
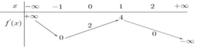
Biết rằng f(-1) = 10 3 , f(2) = 6. Giá trị nhỏ nhất của hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2] bằng
A. 10 3
B. 820 27
C. 730 27
D. 198
Cho X là tập hợp tất cả các giá trị nguyên thuộc đoạn
[
-
5
;
5
]
của tham số m để hàm số
y
x
3
-
3
x
2
+
m
x
-
2
đồng biến trên khoảng
2
;
+
∞
. Số phần tử của X là A. 3 B. 6 C. 2 D. 5
Đọc tiếp
Cho X là tập hợp tất cả các giá trị nguyên thuộc đoạn [ - 5 ; 5 ] của tham số m để hàm số y = x 3 - 3 x 2 + m x - 2 đồng biến trên khoảng 2 ; + ∞ .
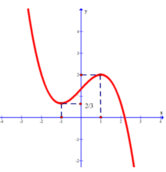
Số phần tử của X là
A. 3
B. 6
C. 2
D. 5
Cho hàm số yf(x) là hàm đa thức với hệ số thực. Hình vẽ bên dưới là một phần đồ thị của hai hàm số: yf(x) và yf(x) Tập các giá trị của tham số m để phương trình
f
(
x
)
m
e
x
có hai nghiệm phân biệt trên [0;2] là nửa khoảng [a;b). Tổng a+b gần nhất với giá trị nào sau đây? A. -0.81 B. -0.54 C. -0.27 D. 0.27
Đọc tiếp
Cho hàm số y=f(x) là hàm đa thức với hệ số thực. Hình vẽ bên dưới là một phần đồ thị của hai hàm số: y=f(x) và y=f'(x)
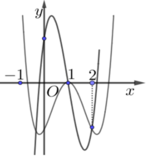
Tập các giá trị của tham số m để phương trình f ( x ) = m e x có hai nghiệm phân biệt trên [0;2] là nửa khoảng [a;b). Tổng a+b gần nhất với giá trị nào sau đây?
A. -0.81
B. -0.54
C. -0.27
D. 0.27
Cho hàm số
y
2
x
+
1
+
1
2
x
-
m
với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng (-50;50) để hàm s...
Đọc tiếp
Cho hàm số y = 2 x + 1 + 1 2 x - m với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng (-50;50) để hàm số nghịch biến trên khoảng (-1;1). Số phần tử của tập hợp S là:
A. 47
B. 48
C. 50
D. 49
Cho hàm số
y
ln
x
-
4
ln
x
-
2
m
với m là tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đồng biến trên khoảng (1;e). Số phần tử của S là A. 2. B. 1. C. 4. D. 3.
Đọc tiếp
Cho hàm số y = ln x - 4 ln x - 2 m với m là tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đồng biến trên khoảng (1;e). Số phần tử của S là
A. 2.
B. 1.
C. 4.
D. 3.