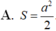Đáp án là B
Diện tích bề mặt của mỗi tầng (kể từ tầng 1) lập thành một cấp số nhân có công bội
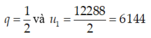
Khi đó diện tích mặt trên cùng là: .
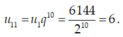
Đáp án là B
Diện tích bề mặt của mỗi tầng (kể từ tầng 1) lập thành một cấp số nhân có công bội
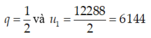
Khi đó diện tích mặt trên cùng là: .
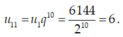
Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích của đế tháp (có diện tích là 12288m2). Tính diện tích mặt trên cùng?
A. 8m2.
B. 6m2.
C. 10m2.
D. 12m2.
Người ta xây dựng một cái tháp gồm 11 tầng. Diện tích bề mặt của mỗi tầng bằng nửa diện tích bề mặt của tầng ngay bên dưới và diện tích bề mặt của tầng một bằng 3 4 diện tích đế tháp. Biết đế tháp có diện tích bằng 12288 m 2 . Diện tích bề mặt của tầng trên cùng là
A. 4 , 5 m 2
B. 18 m 2
C. 9 m 2
D. 16 m 2
Cho tứ diện ABCD và M, N là các điểm thay đổi trên cạnh AB và CD sao cho A M M B = C N N D . Gọi P là một điểm trên cạnh AC và S là diện tích thiết diện cắt bởi mặt phẳng (MNP) và hình chóp. Tính tỉ số k của diện tích tam giác MNP và diện tích thiết diện S
A. 2 k k + 1 .
B. 1 k .
C. k k + 1 .
D. 1 k + 1 .
Một kim tự tháp Ai Cập được xây dựng khoảng 2500 năm trước công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 150m, cạnh đáy dài 220m. Hỏi diện tích xung quanh của kim tự tháp đó bằng bao nhiêu? ( Diện tích xung quanh của hình chóp là tổng diện tích của các mặt bên).
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = 1, AC = 2; cạnh bên SA vuông góc với đáy và SA = 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho A M = x ( 0 < x < 1 ) và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng.
![]()
![]()
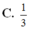
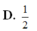
Thiết diện qua trục của một hình nón là tam giác đều cạnh bằng 2. Một mặt cầu có diện tích bằng diện tích toàn phần của hình nón. Tính bán kính của mặt cầu.
![]()
![]()
![]()
![]()
Cho điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của hình chóp tam giác S. ABC sao cho S M M A = 1 2 , S N N B = 2 . Mặt phẳng (α) qua MN và song song với SC chia khối chóp thành 2 phần. Gọi V₁ là thể tích của khối đa diện chứa A, V₂ là thể tích của khối đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 4 5
B. V 1 V 2 = 5 4
C. V 1 V 2 = 5 6
D. V 1 V 2 = 6 5
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C, D và M là trung điểm của đoạn thẳng AB. Gọi T là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T).