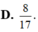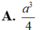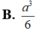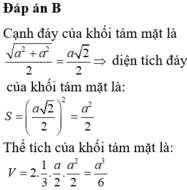Các câu hỏi tương tự
Tính thể tích của khối lập phương có các đỉnh là trọng tâm các mặt của khối bát diện đều cạnh a
Đọc tiếp
Tính thể tích của khối lập phương có các đỉnh là trọng tâm các mặt của khối bát diện đều cạnh a
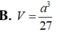
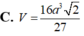
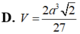
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt Tính bán kính của (S).
Đọc tiếp
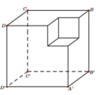
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt ![]() Tính bán kính của (S).
Tính bán kính của (S).
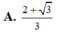
![]()

![]()
Cho hình lập phương cạnh 4cm. Trong khối lập phương là khối cầu tiếp xúc với các mặt của hình lập phương. Tính thể tích phần còn lại của khối lập phương.
Đọc tiếp
Cho hình lập phương cạnh 4cm. Trong khối lập phương là khối cầu tiếp xúc với các mặt của hình lập phương. Tính thể tích phần còn lại của khối lập phương.
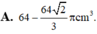
![]()

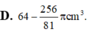
Tổng diện tích các mặt của một khối lập phương là 54
c
m
3
. Tính thể tích của khối lập phương đó.
Đọc tiếp
Tổng diện tích các mặt của một khối lập phương là 54 c m 3 . Tính thể tích của khối lập phương đó.
![]()
![]()
![]()
![]()
Tổng diện tích các mặt của khối lập phương bằng 96 . Tính thể tích của khối lập phương đó
A. 48
B. 84
C. 64
D. 91
Tính thể tích của một khối cầu biết hình lập phương cạnh a nội tiếp trong mặt cầu tạo nên khối cầu đó.
A
.
πa
3
4
B
.
πa
3
2
C
.
πa
3
3
2...
Đọc tiếp
Tính thể tích của một khối cầu biết hình lập phương cạnh a nội tiếp trong mặt cầu tạo nên khối cầu đó.
A . πa 3 4
B . πa 3 2
C . πa 3 3 2
D . πa 3 3 4
Tổng diện tích các mặt của một hình lập phương bằng 150. Thể tích khối lập phương đó là:
A. 200
B. 625
C. 100
D. 125
Một khối lập phương có diện tích một mặt bằng 4. Nếu tăng cạnh của khối lập phương lên gấp đôi thì thể tích khối lập phương đó bằng:
A. 27
B. 64
C. 8
D. 1
Cho khối lập phương ABCD.A’B’C’D’ cạnh a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi
V
1
là thể tích khối chứa điểm A’ và
V
2
là thể tích khối chứa điểm C’. Khi đó
V
1
V
2
là.
Đọc tiếp
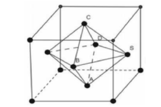
Cho khối lập phương ABCD.A’B’C’D’ cạnh a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi V 1 là thể tích khối chứa điểm A’ và V 2 là thể tích khối chứa điểm C’. Khi đó V 1 V 2 là.
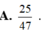
![]()
![]()