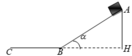
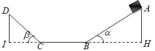
Một vật bắt đầu trượt từ đỉnh một mặt phẳng nghiêng cao 1m, góc nghiêng α=300, sau đó tiếp tục chuyển động trên mặt ngang. Biết hệ số ma sát giữa vật với mặt nghiêng và mặt ngang là như nhau µ= 0,1.
a. Tính vận tốc vật tại chân mặt phẳng nghiêng. Lấy g=10m/s2
b. Quãng đường vật đi được trên mặt ngang.

Định luật ll Niu tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m\cdot\overrightarrow{a}\)
\(Oy:N=Pcos\alpha\)
\(Ox:F-F_{ms}=m\cdot a\)
\(\Rightarrow F-\mu P\cdot cos\alpha=m\cdot a\)
\(\Rightarrow a=\dfrac{F-\mu P\cdot cos\alpha}{m}=\dfrac{P\cdot sin\alpha-\mu P\cdot cos\alpha}{m}\)
\(=\dfrac{10m\cdot sin30^o-0,1\cdot10m\cdot cos30^o}{m}=\dfrac{10-\sqrt{3}}{2}\approx4,13\)m/s
Vận tốc mặt phẳng nghiêng tại chân dốc:
\(v=\sqrt{2al}=\sqrt{2\cdot\dfrac{10-\sqrt{3}}{2}\cdot1}=2,87\)m/s