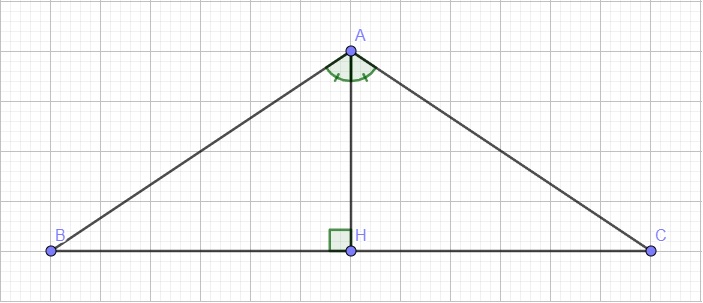
Gọi tam giác đó là ABC với \(\widehat{A}=120^0\) và \(AB=AC=a\)
Kẻ \(AH\perp BC\Rightarrow AH\) đồng thời là đường phân giác và trung tuyến (do ABC cân tại A)
\(\Rightarrow HB=\dfrac{1}{2}BC\) và \(\widehat{BAH}=\dfrac{1}{2}\widehat{A}=\dfrac{1}{2}.120^0=60^0\)
Trong tam giác vuông ABH:
\(cos\widehat{BAH}=\dfrac{AH}{AB}\Rightarrow AH=AB.cos\widehat{BAH}=a.cos60^0=\dfrac{a}{2}\)
\(sin\widehat{BAH}=\dfrac{BH}{AB}\Rightarrow BH=AB.sin\widehat{BAH}=a.sin60^0=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow BC=2BH=a\sqrt{3}\)
\(\Rightarrow S_{\Delta ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{a}{2}.a\sqrt{3}=\dfrac{a^2\sqrt{3}}{4}\)