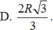Các câu hỏi tương tự
Bạn Hoàn có một tấm bìa hình tròn như hình vẽ, Hoàn muốn biến hình tròn đó thành một cái phễu hình nón. Khi đó Hoàn phải cắt bỏ hình quạt AOB rồi dán hai bán kính OA và OB lại với nhau (diện tích chỗ dán nhỏ không đáng kể). Gọi x là góc ở tâm hình quạt tròn dùng làm phễu. Tìm x để thể tích phễu lớn nhất ?
Đọc tiếp
Bạn Hoàn có một tấm bìa hình tròn như hình vẽ, Hoàn muốn biến hình tròn đó thành một cái phễu hình nón. Khi đó Hoàn phải cắt bỏ hình quạt AOB rồi dán hai bán kính OA và OB lại với nhau (diện tích chỗ dán nhỏ không đáng kể). Gọi x là góc ở tâm hình quạt tròn dùng làm phễu. Tìm x để thể tích phễu lớn nhất ?
![]()
![]()
![]()
Cho hai mặt phẳng (P) và (Q) song song với nhau cắt khối cầu tâm O bán kính R tạo thành hai hình tròn (C1) và (C2) cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn, đáy trùng với hình tròn còn lại. Biết diện tích xung quanh của hình nón là lớn nhất, khi đó thể tích khối trụ có hai đáy là hai hình tròn (C1) và (C2) bằng: A.
4
π
R...
Đọc tiếp
Cho hai mặt phẳng (P) và (Q) song song với nhau cắt khối cầu tâm O bán kính R tạo thành hai hình tròn (C1) và (C2) cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn, đáy trùng với hình tròn còn lại. Biết diện tích xung quanh của hình nón là lớn nhất, khi đó thể tích khối trụ có hai đáy là hai hình tròn (C1) và (C2) bằng:
A. 4 π R 3 3 9
B. 2 π R 3 3 9
C. π R 3 3 9
D. 4 π R 3 3 3
Từ một miếng bìa hình tròn bán kính là 20cm, cắt bỏ hình quạt OAFC phần còn lại ghép thành hình nón như hình vẽ. Biết số đo cung AEC
240
o
. Diện tích xung quanh của nón là: A.
800
3
π
(
cm
2
)
B
.
400
3
π
(...
Đọc tiếp
Từ một miếng bìa hình tròn bán kính là 20cm, cắt bỏ hình quạt OAFC phần còn lại ghép thành hình nón như hình vẽ. Biết số đo cung AEC= 240 o . Diện tích xung quanh của nón là:
A. 800 3 π ( cm 2 )
B . 400 3 π ( cm 2 )
C. 800 5 π ( cm 2 )
D. 400 5 π ( cm 2 )
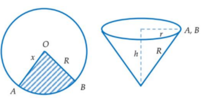
Cắt bỏ hình quạt tròn AOB từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và OB của hình quạt tròn còn lại với nhau để được một cái phễu có dạng của một hình nón. Gọi x là góc ở tâm của quạt tròn dùng làm phễu
0
x
2
π
.Tìm giá trị lớn nhất của thể tích hình nón.
Đọc tiếp
Cắt bỏ hình quạt tròn AOB từ một mảnh các tông hình tròn bán kính R rồi dán hai bán kính OA và OB của hình quạt tròn còn lại với nhau để được một cái phễu có dạng của một hình nón. Gọi x là góc ở tâm của quạt tròn dùng làm phễu 0 < x < 2 π .Tìm giá trị lớn nhất của thể tích hình nón.
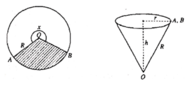
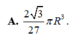
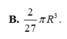
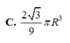
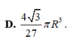
Cho hình trụ có hai đáy là hai hình tròn tâm O và O, bán kính đáy bằng r và một hình nón có đỉnh là O đáy là hình tròn tâm O. Biết diện tích xung quanh của hình nón bằng hai lần diện tích đáy của nó. Tính thể tích V của khối trụ giới hạn bởi hình trụ đã cho.
Đọc tiếp
Cho hình trụ có hai đáy là hai hình tròn tâm O và O', bán kính đáy bằng r và một hình nón có đỉnh là O đáy là hình tròn tâm O'. Biết diện tích xung quanh của hình nón bằng hai lần diện tích đáy của nó. Tính thể tích V của khối trụ giới hạn bởi hình trụ đã cho.
![]()
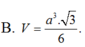
![]()
![]()
Cho hình trụ có hai đáy là hai hình tròn tâm O và O, bán kính đáy bằng r và một hình nón có đỉnh là O đáy là hình tròn tâm O. Biết diện tích xung quanh của hình nón bằng hai lần diện tích đáy của nó. Tính thể tích V của khối trụ giới hạn bởi hình trụ đã cho.
Đọc tiếp
Cho hình trụ có hai đáy là hai hình tròn tâm O và O', bán kính đáy bằng r và một hình nón có đỉnh là O đáy là hình tròn tâm O'. Biết diện tích xung quanh của hình nón bằng hai lần diện tích đáy của nó. Tính thể tích V của khối trụ giới hạn bởi hình trụ đã cho.
![]()
![]()
![]()
![]()
Cho hai mặt phẳng (P) và (Q) song song với nhau và cắt một mặt cầu tâm O bán kính R tạo thành hai đường tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai đường tròn và đáy trùng với đường tròn còn lại. Tính khoảng cách giữa (P) và (Q) để diện tích xung quanh hính nón đó là lớn nhất.
Đọc tiếp
Cho hai mặt phẳng (P) và (Q) song song với nhau và cắt một mặt cầu tâm O bán kính R tạo thành hai đường tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai đường tròn và đáy trùng với đường tròn còn lại. Tính khoảng cách giữa (P) và (Q) để diện tích xung quanh hính nón đó là lớn nhất.
![]()
![]()
![]()
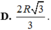
Cho hai mặt phẳng (P) và (Q) song song với nhau và cắt một mặt cầu tâm O bán kính R tạo thành hai đường tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai đường tròn và đáy trùng với đường tròn còn lại. Tính khoảng cách giữa (P) và (Q) để diện tích xung quanh hính nón đó là lớn nhất.
Đọc tiếp
Cho hai mặt phẳng (P) và (Q) song song với nhau và cắt một mặt cầu tâm O bán kính R tạo thành hai đường tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai đường tròn và đáy trùng với đường tròn còn lại. Tính khoảng cách giữa (P) và (Q) để diện tích xung quanh hính nón đó là lớn nhất.
![]()
![]()
![]()
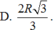
Cho hai mặt phẳng (P) và (Q) song song với nhau và cắt một mặt cầu tâm O bán kính R tạo thành hai đường tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai đường tròn và đáy trùng với đường tròn còn lại. Tính khoảng cách giữa (P) và (Q) để diện tích xung quanh hính nón đó là lớn nhất.
Đọc tiếp
Cho hai mặt phẳng (P) và (Q) song song với nhau và cắt một mặt cầu tâm O bán kính R tạo thành hai đường tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai đường tròn và đáy trùng với đường tròn còn lại. Tính khoảng cách giữa (P) và (Q) để diện tích xung quanh hính nón đó là lớn nhất.
![]()
![]()
![]()