Một ô tô có khối lượng 2 tấn khi đi qua A có vận tốc 72 km/h thì tài xế tắt máy, xe chuyển động chậm dần đều đến B thì có vận tốc 18km/h. Biết quãng đường AB nằm ngang dài 100m.
a, Xác định hệ số ma sát μ 1 trên đoạn đường AB.
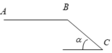
b, Đến B xe vẫn không nổ máy và tiếp tục xuống dốc nghiêng BC dài 50m, biết dốc hợp với mặt phẳng nằm ngang một góc α = 30 0 . Biết hệ sồ ma sát giữa bánh xe và dốc nghiêng là μ 2 = 0 , 1 . Xác định vận tốc của xe tại chân dốc nghiêng C.
a. Ta có v A = 72 ( k m / h ) = 20 ( m / s ) ; v B = 18 ( k m / h ) = 5 ( m / s )
Chọn mốc thế năng tại AB
Theo định luật bảo toàn năng lượng W A = W B + A m s
W A = 1 2 m v A 2 = 1 2 .2000.20 2 = 4.10 5 ( J ) W B = 1 2 m v B 2 = 1 2 .2000.5 2 = 25000 ( J ) A m s = μ 1 . m . g . A B = μ 1 .2000.10.100 = 2.10 6 . μ 1 ( J ) ⇒ 4.10 5 = 25000 + 2.10 6 . μ 1 ⇒ μ 1 = 0 , 1875
b. Chọn mốc thế năng tại C
z B = B C . sin 30 0 = 50.0 , 5 = 25 ( m )
Theo định luật bảo toàn năng lượng W B = W C + A m s
W B = 1 2 m v B 2 + m g z B = 1 2 .2000.5 2 + 2000.10.25 = 525000 ( J ) W C = 1 2 m v C 2 = 1 2 .2000. v C 2 = 1000. v C 2 ( J )
A m s = μ 2 . m . g . cos 30 0 . B C = 0 , 1.2000.10. 3 2 .50 = 86602 , 54 ( J ) ⇒ 525000 = 1000 v C 2 + 86602 , 54 ⇒ v C = 20 , 94 ( m / s )




