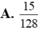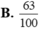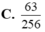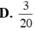Các câu hỏi tương tự
Trong không gian với hệ toạ độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục toạ độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc toạ độ sao cho M là trực tâm của tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục toạ độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc toạ độ sao cho M là trực tâm của tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
![]()
![]()
![]()
![]()
Trong hệ trục toạ độ Oxyz, cho điểm H(2;1;2). Điểm H là hình chiếu vuông góc của gốc toạ độ O xuống mặt phẳng (P), số đo góc giữa mặt phẳng (P) và mặt phẳng (Q): x+y-110 là A. 90
°
B. 30
°
C. 60
°
D. 45
°
Đọc tiếp
Trong hệ trục toạ độ Oxyz, cho điểm H(2;1;2). Điểm H là hình chiếu vuông góc của gốc toạ độ O xuống mặt phẳng (P), số đo góc giữa mặt phẳng (P) và mặt phẳng (Q): x+y-11=0 là
A. 90 °
B. 30 °
C. 60 °
D. 45 °
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) đi qua gốc toạ độ và nhận (3;2;1) là véctơ pháp tuyến. Phương trình của mặt phẳng (P) là: A. 3x+2y+z-140 B. 3x+2y+z0 C. 3x+2y+z+20 D. x+2y+3z0.
Đọc tiếp
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) đi qua gốc toạ độ và nhận ![]() =(3;2;1) là véctơ pháp tuyến. Phương trình của mặt phẳng (P) là:
=(3;2;1) là véctơ pháp tuyến. Phương trình của mặt phẳng (P) là:
A. 3x+2y+z-14=0
B. 3x+2y+z=0
C. 3x+2y+z+2=0
D. x+2y+3z=0.
Trong không gian với hệ toạ độ Oxyz, gọi (α) là mặt phẳng qua
G
(
1
;
2
;
3
)
và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A,B, C (khác gốc O) sao cho G là trọng tâm của tam giác ABC. Khi đó mặt phẳng (α) có phương trình: A. 3x + 6y + 2z + 18 0 B. 6x + 3y + 2z - 18 0 C. 2x + y + 3z - 9 0 D. 6x + 3y + 2z + 9 0
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, gọi (α) là mặt phẳng qua G ( 1 ; 2 ; 3 ) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A,B, C (khác gốc O) sao cho G là trọng tâm của tam giác ABC. Khi đó mặt phẳng (α) có phương trình:
A. 3x + 6y + 2z + 18 = 0
B. 6x + 3y + 2z - 18 = 0
C. 2x + y + 3z - 9 = 0
D. 6x + 3y + 2z + 9 = 0
Trong không gian với hệ trục toạ độ Oxyz, cho hai điểm A(-1;3;4), B(9;-7;2). Tìm trên trục Ox toạ độ điểm M sao cho
M
A
2
+
M
B
2
đạt giá trị nhỏ nhất A. M(5;0;0) B. M(-2;0;0) C. M(4;0;0) D. M(9;0;0)
Đọc tiếp
Trong không gian với hệ trục toạ độ Oxyz, cho hai điểm A(-1;3;4), B(9;-7;2). Tìm trên trục Ox toạ độ điểm M sao cho M A 2 + M B 2 đạt giá trị nhỏ nhất
A. M(5;0;0)
B. M(-2;0;0)
C. M(4;0;0)
D. M(9;0;0)
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng
P
:
6
x
+
3
y
-
2
z
+
24
0
và điểm A(2;5;1). Tìm toạ độ hình chiếu vuông góc H của A trên (P). A. H(4;2;3) B. H(4;2;-3) C. H(4;-2;3) D. H(-4;2;3)
Đọc tiếp
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng P : 6 x + 3 y - 2 z + 24 = 0 và điểm A(2;5;1). Tìm toạ độ hình chiếu vuông góc H của A trên (P).
A. H(4;2;3)
B. H(4;2;-3)
C. H(4;-2;3)
D. H(-4;2;3)
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng
P
:
6
x
+
3
y
-
2
z
+
24
0
và điểm A(2;5;1). Tìm toạ độ hình chiếu vuông góc H của A trên (P). A. H(4;2;3) B. H(4;2;-3) C. H(4;-2;3) D. H(-4;2;3)
Đọc tiếp
Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng P : 6 x + 3 y - 2 z + 24 = 0 và điểm A(2;5;1). Tìm toạ độ hình chiếu vuông góc H của A trên (P).
A. H(4;2;3)
B. H(4;2;-3)
C. H(4;-2;3)
D. H(-4;2;3)
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2;-3;2), B (3;5;4). Tìm toạ độ điểm M trên trục Oz sao cho MA²+MB² đạt giá trị nhỏ nhất.
A. M (0;0;49)
B. M (0;0;67)
C. M (0;0;3)
D. M (0;0;0).
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2;-3;2), B (3;5;4). Tìm toạ độ điểm M trên trục Oz so cho MA²+MB² đạt giá trị nhỏ nhất. A. M (0;0;49) B. M (0;0;67) C. M (0;0;3) D. M (0;0;0)
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2;-3;2), B (3;5;4). Tìm toạ độ điểm M trên trục Oz so cho MA²+MB² đạt giá trị nhỏ nhất.
A. M (0;0;49)
B. M (0;0;67)
C. M (0;0;3)
D. M (0;0;0)