Các câu hỏi tương tự
Một mặt cầu có diện tích bằng 36π c m 2 thì bán kính của nó bằng:
A. 4 cm
B. 3 cm
C. 6 cm
D. 5 cm
Với nửa hình cầu bán kính r và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng h. Khi h = 12 (cm) và tổng diện tích nửa mặt cầu và diện tích “hình tròn đáy” gấp ba lần diện tích toàn phần của hình trụ thì r (cm) bằng bao nhiêu?
Một hình cầu đặt vừa khít vào trong một hình trụ như hình bên (chiều cao của hình trụ bằng độ dài đường kính của hình cầu) thì thể tích của nó bằng 2/3 thể tích của hình trụ.Nếu đường kính của hình cầu là d (cm) thì thể tích của hình trụ là:A. (1/4).
πd
3
cm
3
B. (1/3).
πd
3
cm...
Đọc tiếp
Một hình cầu đặt vừa khít vào trong một hình trụ như hình bên (chiều cao của hình trụ bằng độ dài đường kính của hình cầu) thì thể tích của nó bằng 2/3 thể tích của hình trụ.
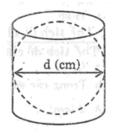
Nếu đường kính của hình cầu là d (cm) thì thể tích của hình trụ là:
A. (1/4). πd 3 cm 3 B. (1/3). πd 3 cm 3
C.(2/3). πd 3 cm 3 D. (3/4). πd 3 cm 3
Cho một hình nón có bán kính đường tròn đáy là r (cm), chiều cao 2r (cm) và một hình cầu có bán kính r (cm). Hãy tính:a, Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06
c
m
2
b, Thể tích của hình nón, biết thể tích của hình cầu là 15,8
c
m
3
Đọc tiếp
Cho một hình nón có bán kính đường tròn đáy là r (cm), chiều cao 2r (cm) và một hình cầu có bán kính r (cm). Hãy tính:
a, Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06 c m 2
b, Thể tích của hình nón, biết thể tích của hình cầu là 15,8 c m 3
Cho hai hình cầu A và B lần lượt có bán kính là 3 cm và 6 cm. So sánh diện tích hai mặt cầu của hai hình cầu đó là: A.
S
A
S
B
B.
S
A
2
S
B
C.
S
A
1
2
S...
Đọc tiếp
Cho hai hình cầu A và B lần lượt có bán kính là 3 cm và 6 cm. So sánh diện tích hai mặt cầu của hai hình cầu đó là:
A. S A = S B
B. S A = 2 S B
C. S A = 1 2 S B
D. S A = 1 4 S B
Một hình cầu có bán kính bằng 5cm. Một hình nón cũng có bán kính bằng 5cm và có diện tích toàn phần bằng diện tích mặt cầu. Tính chiều cao của hình nón
Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính:Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06
c
m
2
Đọc tiếp
Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính:
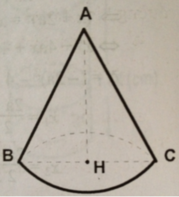
Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06 c m 2
Một hình cầu có bán kính 5cm. Một hình nón cũng có bán kính đáy là 5cm. Và có diện tích tp bằng diện tích mặt cầu. Tính chiều cao của nón
Một vật thể dạng hình trụ bán kính đường tròn đáy và độ dài của nó đều bằng 2r (cm). Người ta khoan một lỗ cũng có dạng hình trụ như hình sau, có bán kính đáy và độ sâu đều bằng r(cm) .Thể tích phần vật thể còn lại (tính theo
c
m
3
) là:A.4π
r
3
B.7π
r
3
C.8π...
Đọc tiếp
Một vật thể dạng hình trụ bán kính đường tròn đáy và độ dài của nó đều bằng 2r (cm). Người ta khoan một lỗ cũng có dạng hình trụ như hình sau, có bán kính đáy và độ sâu đều bằng r(cm) .Thể tích phần vật thể còn lại (tính theo c m 3 ) là:
A.4π r 3 B.7π r 3 C.8π r 3 D.9π r 3