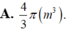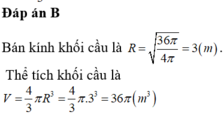Các câu hỏi tương tự
Cho một khối cầu có thể tích bằng
500
π
3
. Tính diện tích S của mặt cầu đó.
Đọc tiếp
Cho một khối cầu có thể tích bằng 500 π 3 . Tính diện tích S của mặt cầu đó.
Một khối cầu có thể tích Tính diện tích S của mặt cầu tương ứng
Đọc tiếp
Một khối cầu có thể tích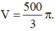 
Tính diện tích S của mặt cầu tương ứng
Một hình cầu có bán kính bằng 2(m). Hỏi diện tích của mặt cầu bằng bao nhiêu A. 4
π
(
m
2
)
B. 16
π
(
m
2
)
C. 8
π
(
m
2
)
D.
π
(
m
2...
Đọc tiếp
Một hình cầu có bán kính bằng 2(m). Hỏi diện tích của mặt cầu bằng bao nhiêu
A. 4 π ( m 2 )
B. 16 π ( m 2 )
C. 8 π ( m 2 )
D. π ( m 2 )
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kỳ nội tiếp mặt cầu (S) Thể tích khối nón (H) là
V
1
thể tích phần còn lại của khối cầu là
V
2
Giá trị lớn nhất của
V
1
V
2
bằng: A.
81
32
B.
76
32...
Đọc tiếp
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kỳ nội tiếp mặt cầu (S) Thể tích khối nón (H) là V 1 thể tích phần còn lại của khối cầu là V 2 Giá trị lớn nhất của V 1 V 2 bằng:
A. 81 32
B. 76 32
C. 32 81
D. 32 76
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc
60
o
Gọi (S ) là mặt cầu ngoại tiếp hình chóp S.ABC. Thể tích của khối cầu tạo nên bởi mặt cầu (S ) bằng
Đọc tiếp
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 60 o Gọi (S ) là mặt cầu ngoại tiếp hình chóp S.ABC. Thể tích của khối cầu tạo nên bởi mặt cầu (S ) bằng
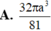
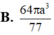
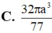
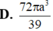
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S)bằng
Đọc tiếp
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S)bằng
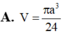
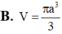
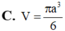
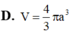
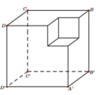
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt Tính bán kính của (S).
Đọc tiếp
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt 
Tính bán kính của (S).
Một khối trụ có đường kính đáy bằng chiều cao và nội tiếp trong mặt cầu bán kính R thì thể tích của khối trụ là: A.
2
πR
3
B.
πR
3
2
2
C.
πR
3
2
6...
Đọc tiếp
Một khối trụ có đường kính đáy bằng chiều cao và nội tiếp trong mặt cầu bán kính R thì thể tích của khối trụ là:
A. 2 πR 3
B. πR 3 2 2
C. πR 3 2 6
D. 2 πR 3 3
Cho mặt cầu (S) bán kính R. Hình nón (N) thay đổi có đỉnh và đường tròn đáy thuộc mặt cầu (S) Tính thể tích lớn nhất của khối nón (N) đổi có đỉnh và đường tròn đáy thuộc mặt cầu (S) Tính thể tích lớn nhất của khối nón (N) A.
32
πR
3
81
B.
32
R
3
81...
Đọc tiếp
Cho mặt cầu (S) bán kính R. Hình nón (N) thay đổi có đỉnh và đường tròn đáy thuộc mặt cầu (S) Tính thể tích lớn nhất của khối nón (N) đổi có đỉnh và đường tròn đáy thuộc mặt cầu (S) Tính thể tích lớn nhất của khối nón (N)
A. 32 πR 3 81
B. 32 R 3 81
C. 32 πR 3 27
D. 32 R 3 27