Các câu hỏi tương tự
Trên một mảnh đất hình vuông có diện tích
81
m
2
người ta đào một cái ao nuôi cá hình trụ (như hình vẽ) sao cho tâm của hình tròn đáy trùng với tâm của mảnh đất. Ở giữa mép ao và mép mảnh đất người ta để lại một khoảng đất trống để đi lại, biết khoảng cách nhỏ nhất giữa mép ao và mép mảnh đất là x(m). Giả sử chiều sâu của ao cũng là x(m). Tính thể tích lớn nhất của ao. A. ...
Đọc tiếp
Trên một mảnh đất hình vuông có diện tích 81 m 2 người ta đào một cái ao nuôi cá hình trụ (như hình vẽ) sao cho tâm của hình tròn đáy trùng với tâm của mảnh đất. Ở giữa mép ao và mép mảnh đất người ta để lại một khoảng đất trống để đi lại, biết khoảng cách nhỏ nhất giữa mép ao và mép mảnh đất là x(m). Giả sử chiều sâu của ao cũng là x(m). Tính thể tích lớn nhất của ao.

A. V = 13 , 5 π ( c m 3 )
B. V = 27 π ( c m 3 )
C. V = 36 π ( c m 3 )
D. V = 72 π ( c m 3 )
Một vật thể có mặt đáy nằm trong mặt phẳng tọa độ (Oxy) được giới hạn bởi đường cong
y
2
4
x
và đường thẳng x 4. Thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox là một nửa hình elip có trục lớn gấp đôi trục nhỏ. Tính thể tích của vật thể A.
8
π
B.
16
π
C.
32
π
D.
64
π
Đọc tiếp
Một vật thể có mặt đáy nằm trong mặt phẳng tọa độ (Oxy) được giới hạn bởi đường cong y 2 = 4 x và đường thẳng x = 4. Thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox là một nửa hình elip có trục lớn gấp đôi trục nhỏ. Tính thể tích của vật thể
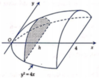
A. 8 π
B. 16 π
C. 32 π
D. 64 π
Cho hình nón (N) có đường cao SOh và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OMx, 0xh. (C) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất.
Đọc tiếp
Cho hình nón (N) có đường cao SO=h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OM=x, 0<x<h. (C) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất.
![]()
![]()
![]()
![]()
Cho hình nón (N) có đường cao SO h và bán kính đáy bằng R , gọi M là điểm trên đoạn SO , đặt OM x, 0xh. (C) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M , với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất.
Đọc tiếp
Cho hình nón (N) có đường cao SO = h và bán kính đáy bằng R , gọi M là điểm trên đoạn SO , đặt OM = x, 0<x<h. (C) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M , với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất.
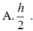
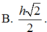
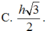
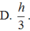
Cho hình nón (N) có đường cao SO h và bán kính đáy bằng R , gọi M là điểm trên đoạn SO , đặt OM x, 0xh. (C) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M , với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất.
Đọc tiếp
Cho hình nón (N) có đường cao SO = h và bán kính đáy bằng R , gọi M là điểm trên đoạn SO , đặt OM = x, 0<x<h. (C) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M , với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất.
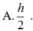
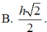
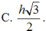
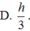
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB 1, AC 2; cạnh bên SA vuông góc với đáy và SA 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho
A
M
x
(
0
x
1
)
và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng.
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = 1, AC = 2; cạnh bên SA vuông góc với đáy và SA = 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho A M = x ( 0 < x < 1 ) và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng.
![]()
![]()
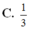
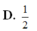
Cho hình thang cân ABCD có đáy nhỏ AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất
S
m
a
x
của hình thang.
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất S m a x của hình thang.
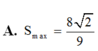
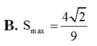
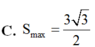
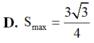
giúp mình bài này gấp vs ạ
1. tìm họ nguyên hàm của hàm số f(x) = ( 1 + ln x)^2 / x
2. cho hình nón đỉnh S có đáy là hình tròn tâm O. mặt phẳng ( P ) qua S và O cắt hình nón theo thiết diện là một tam giác vuông có diện tích = 2. Tính thể tích khối nón được giới hạn bởi hình nón đã cho
Cho hình chóp S.ABC có đáy ABC vuông cân tại B với AB a, SA
a
3
và
S
A
⊥
A
B
C
. Gọi M là điểm trên cạnh AB và AM x (0 x a), mặt phẳng
α
đi qua M và vuông góc với AB. Tìm x để diện tích thiết diện tạo bởi mặt phẳng
α
và hình chóp S.ABC lớn nhất
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC vuông cân tại B với AB = a, SA = a 3 và S A ⊥ A B C . Gọi M là điểm trên cạnh AB và AM = x (0 < x < a), mặt phẳng α đi qua M và vuông góc với AB. Tìm x để diện tích thiết diện tạo bởi mặt phẳng α và hình chóp S.ABC lớn nhất
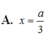

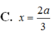
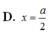
Cho hình thang cân ABCD có đáy nhỏ AB. Biết AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất của hình thang A.
8
2
9
B.
4
2
9
C.
3
3
2
D.
3
3...
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ AB. Biết AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất của hình thang
A. 8 2 9
B. 4 2 9
C. 3 3 2
D. 3 3 4



