Các câu hỏi tương tự
Một khối nón và một khối trụ có chiều cao và bán kính đáy đều bằng 1. Tổng thể tích của khối nón và khối trụ đó là A.
2
π
3
B.
4
π
3
C. ...
Đọc tiếp
Một khối nón và một khối trụ có chiều cao và bán kính đáy đều bằng 1. Tổng thể tích của khối nón và khối trụ đó là
A. 2 π 3
B. 4 π 3
C. 10 π 3
D. 4 π
Cho khối trụ có chiều cao h 3 và diện tích toàn phần bằng 20
π
. Khi đó chu vi đáy của khối trụ là
Đọc tiếp
Cho khối trụ có chiều cao h = 3 và diện tích toàn phần bằng 20 π . Khi đó chu vi đáy của khối trụ là
![]()
![]()
![]()
![]()
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h3 là chiều cao. Biết thể tích khối nón cụt là
V
π
tìm giá trị lớn nhất của biểu thức PR+2r A.
2
3
B. 3. C.
3
3
D. 2.
Đọc tiếp
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h=3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P=R+2r
A. 2 3
B. 3.
C. 3 3
D. 2.
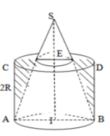
Cho hình nón có độ dài đường kính đáy là 2R, độ dài đường sinh là
R
17
và hình trụ có chiều cao và đường kính đáy đều bằng 2R, lồng vào nhau như hình vẽ bên. Tính thể tích phần khối trụ không giao với khối nón
Đọc tiếp
Cho hình nón có độ dài đường kính đáy là 2R, độ dài đường sinh là R 17 và hình trụ có chiều cao và đường kính đáy đều bằng 2R, lồng vào nhau như hình vẽ bên. Tính thể tích phần khối trụ không giao với khối nón
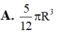
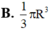
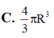
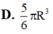
Trong các khối trụ có cùng diện tích toàn phần bằng
π
. Gọi (T) là khối trụ có thể tích lớn nhất, chiều cao của (T) bằng
Đọc tiếp
Trong các khối trụ có cùng diện tích toàn phần bằng π . Gọi (T) là khối trụ có thể tích lớn nhất, chiều cao của (T) bằng
![]()
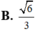
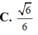
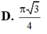
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
Đọc tiếp
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).

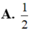
![]()
![]()
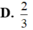
Một khối trụ (N) có diện tích xung quanh bằng
4
π
3
và chiều cao là một số nguyên ngoại tiếp một khối nón (N) có đường sinh bằng
7
. Tính thể tích V phần không gian bên ngoài khối nón và bên trong khối trụ.
Đọc tiếp
Một khối trụ (N) có diện tích xung quanh bằng 4 π 3 và chiều cao là một số nguyên ngoại tiếp một khối nón (N') có đường sinh bằng 7 . Tính thể tích V phần không gian bên ngoài khối nón và bên trong khối trụ.
![]()
![]()
![]()
![]()
Cho khối nón có bán kính đáy r
3
và chiều cao h4 Tính thể tích V của khối nón đã cho.
Đọc tiếp
Cho khối nón có bán kính đáy r = 3 và chiều cao h=4 Tính thể tích V của khối nón đã cho.
![]()
![]()
![]()
![]()
Cho khối nón có bán kính đáy r
3
và chiều cao h4 Tính thể tích V của khối nón đã cho.
Đọc tiếp
Cho khối nón có bán kính đáy r= 3 và chiều cao h=4 Tính thể tích V của khối nón đã cho.
![]()
![]()
![]()
![]()



