Đáp án D
Phương pháp:
Diện tích xung quanh của khối nón: Sxq = πRl
Cách giải:
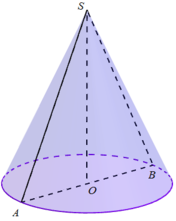
Theo đề bài, ta có tam giác SAB là tam giác vuông cân tại S, SO = a ⇒ R = OA = SO = a

Đáp án D

Phương pháp:
Diện tích xung quanh của khối nón: Sxq = πRl
Cách giải:
Theo đề bài, ta có tam giác SAB là tam giác vuông cân tại S, SO = a ⇒ R = OA = SO = a

Một hình nón có chiều cao bằng a và thiết diện qua trục của hình nón đó là tam giác vuông. Tính theo a diện tích xung quanh của hình nón đó
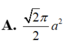
![]()
![]()
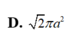
Cho một hình nón với thiết diện qua trục là một tam giác đều cạnh 2a có diện tích xung quanh là S 1 và một mặt cầu có đường kính bằng chiều cao hình nón có diện tích là S 2 . Khi đó, hệ thức giữa S 1 và S 2 là:
A. S 1 = S 2 B. S 1 = 4 S 2
C. S 2 = 2 S 1 D. 2 S 2 = 3 S 1
Một hình nón tròn xoay mà thiết diện tạo bởi mặt phẳng chứa trục hình nón với hình nón là một tam giác vuông cân có diện tích bằng 4 a 2 (a>2). Tính diện tích xung quanh S x q của hình nón
![]()
![]()
![]()
![]()
Hình nón có thiết diện cắt bởi mặt phẳng qua trục là một tam giác vuông và có diện tích xung quanh là 2 . Độ dài đường cao của hình nón là:
A. 2
B. 1
C. 1/ 2
D. 2
Cho hình nón có thiết diện qua trục là một tam giác vuông cân có độ dài cạnh huyền bằng 2. Diện tích xung quanh của hình nón bằng
![]()
![]()
![]()
![]()
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Tính diện tích xung quanh của hình nón.
A. πa 2 2 4
B. πa 2 2 2
C. πa 2 2
D. 2 πa 2 2 3
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Tính diện tích xung quanh của hình nón
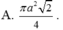
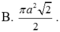
![]()
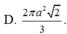
Cho hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón là:
A. πa 2 2 B. πa 2 2 4
C. πa 2 2 2 D. 2 πa 2 2 3
Cắt một hình nón bằng một mặt phẳng đi qua trục của nó ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng a, diện tích xung quanh của hình nón đó là:
![]()
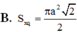
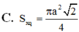
![]()