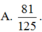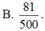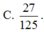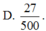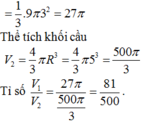Các câu hỏi tương tự
Gọi r và h lần lượt là bán kính đáy và chiều cao của một hình nón. Kí hiệu
V
1
,
V
2
lần lượt là thể tích hình nón và thể tích hình cầu nội tiếp hình nón. Khi r và h thay đổi, tìm giá trị bé nhất của tỉ số
V
1
V
2
Đọc tiếp
Gọi r và h lần lượt là bán kính đáy và chiều cao của một hình nón. Kí hiệu V 1 , V 2 lần lượt là thể tích hình nón và thể tích hình cầu nội tiếp hình nón. Khi r và h thay đổi, tìm giá trị bé nhất của tỉ số V 1 V 2
![]()
![]()
![]()
![]()
Cho khối nón có độ lớn góc ở đỉnh là
π
3
. Một khối cầu
(
S
1
)
nội tiếp trong khối nón. Gọi
S
2
là khối cầu tiếp xúc với tất cả các đường sinh của nón và với
S
1
;
S
3...
Đọc tiếp
Cho khối nón có độ lớn góc ở đỉnh là π 3 . Một khối cầu ( S 1 ) nội tiếp trong khối nón. Gọi S 2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S 1 ; S 3 là khối tiếp xúc với tất cả các đường sinh của nón với S 1 ;..; S n là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S n - 1 . Gọi V 1 , V 2 , V 3 , . . . . . , V n - 1 , V n , lần lượt là thể tích của khối cầu S 1 , S 2 , S 3 , . . . . . , S n - 1 , S n , và V là thể tích của khối nón. Tính giá trị của biểu thức T = l i m V 1 + V 2 + . . . + V n V .
![]()
![]()
Hình nón tròn xoay nội tiếp trong mặt cầu bán kính R với chiều cao hình nón bằng
3
R
2
. Tính thể tích V của hình nón.
Đọc tiếp
Hình nón tròn xoay nội tiếp trong mặt cầu bán kính R với chiều cao hình nón bằng 3 R 2 . Tính thể tích V của hình nón.
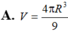
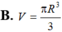
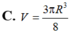
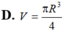
Cho một hình cầu nội tiếp hình nón tròn xoay có góc ở đỉnh là
2
α
, bán kính đáy là R và chiều cao là h. Một hình trụ ngoại tiếp hình cầu đó có đáy dưới nằm trong mặt phẳng đáy của hình nón (tham khảo hình vẽ). Gọi
V
1
,
V
2
lần lượt là thể tích của hình nón và hình trụ, biết rằng ...
Đọc tiếp
Cho một hình cầu nội tiếp hình nón tròn xoay có góc ở đỉnh là 2 α , bán kính đáy là R và chiều cao là h. Một hình trụ ngoại tiếp hình cầu đó có đáy dưới nằm trong mặt phẳng đáy của hình nón (tham khảo hình vẽ). Gọi V 1 , V 2 lần lượt là thể tích của hình nón và hình trụ, biết rằng V 1 ≠ V 2 . Gọi là giá trị lớn nhất của tỉ số V 2 V 1 . Giá trị của biểu thức P=48M+25 thuộc khoảng nào dưới đây?
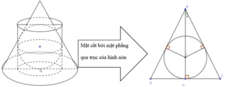
A. (40;60)
B. (60,80)
C. (20,40)
D. (0,20)
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó. Thể tích của khối nón theo r và h.
Cho hình nón (N) có bán kính đáy r20(cm), chiều cao h60(cm) và một hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?
Đọc tiếp
Cho hình nón (N) có bán kính đáy r=20(cm), chiều cao h=60(cm) và một hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?
![]()
![]()
![]()
![]()
Cho khối cầu tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính đáy r, nội tiếp khối cầu. Tính chiều cao h theo bán kính R sao cho khối nón có thể tích lớn nhất.
Đọc tiếp
Cho khối cầu tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính đáy r, nội tiếp khối cầu. Tính chiều cao h theo bán kính R sao cho khối nón có thể tích lớn nhất.
![]()
![]()
![]()
![]()
Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là a và 2a sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Tính bán kính đáy r của hình nón đã cho. A.
r
8
a
3
B.
r
2
2
a
C.
r
4...
Đọc tiếp
Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là a và 2a sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Tính bán kính đáy r của hình nón đã cho.
A. r = 8 a 3
B. r = 2 2 a
C. r = 4 a 3
D. r = 2 a
Một bình đựng nước dạng hình nón (không có đáy), đừng đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là
18
π
dm
3
.Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên). Thể tích V của nước còn lại trong bình bằng: A. 3 B. 8 C. 2 D. 4
Đọc tiếp
Một bình đựng nước dạng hình nón (không có đáy), đừng đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là 18 π dm 3 .Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên). Thể tích V của nước còn lại trong bình bằng:
A. 3
B. 8
C. 2
D. 4