Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Chọn A
Khối đa diện đều có số mặt bằng 12 là khối thập nhị diện đều.
Khi đó số đỉnh của khối này thỏa 2 C = 3 D ⇔ D = 20 .
*Nhắc lại: Khối đa diện đều loại n , p có C cạnh, M mặt và D đỉnh thì 2 C = n M = p D .
Khối đa diện 12 mặt đều có số đỉnh và số cạnh lần lượt là
A. 30 và 20
B. 12 và 20
C. 20 và 30
D. 12 và 30
Khối đa diện có mười hai mặt đều có số đỉnh, số cạnh, số mặt lần lượt là:
A. 30, 20, 12
B. 20, 12, 30
C. 12, 30, 20
D. 20, 30, 12
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V .
A. 7 2 a 3 216
B. 11 2 a 3 216
C. 13 2 a 3 216
D. 2 a 3 18
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của các tam giác ABD, ABC và E là điểm đối xứng với điểm B qua điểm D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V
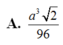
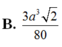
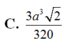
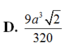
Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hình đa diện (H) có các mặt là nhứng tam giác, mỗi đỉnh là đỉnh chung của đúng 3 mặt. Gọi số các đỉnh, cạnh, mặt của hình đa diện (H) lần lượt là d, c, m. Khi đó:
A. d > m
B. d < m
C. d = m
D. d + m = c
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh A ' B ' và sao cho M A ' = M B ' và N B = 2 N C . Mặt phẳng D M N chia khối lập phương đã cho thành hai khối đa diện. Gọi V H là thể tích khối đa diện chứa đỉnh A , V H ' là thể tích khối đa diện còn lại. Tỉ số V H V H ' bằng
A. 151 209
B. 209 360
C. 2348 3277
D. 151 360
Cho khối chóp tứ giác đều S.ABCD. Gọi M là trung điểm SC, mặt phẳng (P) chứa AM và song song với BD chia khối chóp thành 2 khối đa diện. Đặt V 1 là thể tích khối đa diện có chứa đỉnh S và V 2 là thể tích khối đa diện có chứa đáy. Tỉ số V 1 V 2 bằng:
A. V 1 V 2 = 3 2
B. V 1 V 2 = 1 2
C. V 1 V 2 = 2 3
D. V 1 V 2 = 1
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho một khối đa diện lồi có 10 đỉnh, 7 mặt. Hỏi khối đa diện này có mấy cạnh?
A. 20.
B. 18.
C. 15.
D. 12.
