Một chiếc thùng nặng m = 50 kg đang nằm yên trên sàn ngang thì được kéo bằng một lực F = 220 N theo phương nằm ngang. Hệ số ma sát trượt giữa thùng và mặt sàn là µ = 0,4. Lấy g = 10 m/s2 .
a) Tính độ lớn lực ma sát trượt giữa thùng và mặt sàn.
b) Tính gia tốc của thùng.
c) Sau 10 giây kể từ khi bắt đầu di chuyển, thùng trượt được quãng đường bằng bao nhiêu?
d) Tính vận tốc của thùng sau khi di chuyển được 2 giây.
a) Do vật di chuyển theo phương ngang nên \(N=P=mg=50.10=500\left(N\right)\)
Ta có \(F_{ms}=\mu N=0,4.500=200\left(N\right)\)
b) Áp dụng định luật II Newton, ta có \(\overrightarrow{F}=m\overrightarrow{a}\)
Chiếu lên phương chuyển động của vật, ta có
\(F_k-F_{ms}=ma\) \(\Leftrightarrow a=\dfrac{F_k-F_{ms}}{m}=\dfrac{220-200}{50}=0,4\left(m/s^2\right)\)
c) Quãng đường thùng dịch chuyển: \(s=\dfrac{1}{2}at^2=\dfrac{1}{2}.0,4.10^2=20\left(m\right)\)
d) Vận tốc của vật sau khi di chuyển được 2 giây: \(v=at=0,4.2=0,8\left(m/s\right)\)
a)
Độ lớn lực ma sát trượt giữa thùng và mặt sàn:
\(F_{mst}=\mu.N=0,4.50.10=200\left(N\right)\)
b)
Gia tốc của thùng: \(a=\dfrac{F}{m}=\dfrac{F_{kéo}-F_{ms}}{m}=\dfrac{220-200}{50}=0,4\left(m/s^2\right)\)
(Chiếu theo chiều chuyển động)
c)
Sau 10s kể từ khi bắt đầu di chuyển, thùng trượt được quãng đường:
\(s_{10}=\dfrac{1}{2}.0,4.10^2=20\left(m\right)\)
d)
Vận tốc của thùng sau khi di chuyển được 2s:
\(v=at=0,4.2=0,8\left(m/s\right)\)
Ở đây ta kí hiệu \(N,P,F_k,F_{ms}\) lần lượt là phản lực mặt sàn tác dụng lên thùng; trong lực của thùng; lực kéo, lực ma sát tác dụng lên vật. Chọn chiều (+) là chiều chuyển động của vật.








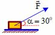
 hợp với hướng chuyển động một góc α = 30° (Hình vẽ). Hệ số ma sát trượt giữa vật và sàn là μt = 0,30. Cho biết độ lớn lực kéo F = 17N và gia tốc trọng trường g = 10m/
s
2
hợp với hướng chuyển động một góc α = 30° (Hình vẽ). Hệ số ma sát trượt giữa vật và sàn là μt = 0,30. Cho biết độ lớn lực kéo F = 17N và gia tốc trọng trường g = 10m/
s
2
