Đáp án A
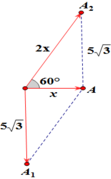
Áp dụng định lý hàm cosin cho tam giác:
( 5 3 ) 2 = ( 2 x ) 2 + x 2 − 2.2 x . x . c os 60 ⇔ x = 5 ( c m )
Suy ra A = 5 ( c m ) .
Đáp án A

Áp dụng định lý hàm cosin cho tam giác:
( 5 3 ) 2 = ( 2 x ) 2 + x 2 − 2.2 x . x . c os 60 ⇔ x = 5 ( c m )
Suy ra A = 5 ( c m ) .
Một chất điểm tham gia đồng thời hai dao động điều hòa cùng tần số trên trục Ox. Biết dao động thành phần thứ nhất có biên độ A 1 = 4 3 , dao động tổng hợp có biên độ A = 4cm. Dao động thành phần thứ hai sớm pha hơn dao động tổng hợp và π 3 . Dao động thành phần thứ hai có biên độ là:
A. 4 cm
B. 4 3 cm
C. 6 3 cm
D. 8 cm
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số. Biết dao động thứ nhất có biên độ A1 = 6 cm và trễ pha π / 2 so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ 9 cm. Biên độ dao động tổng hợp bằng
A. 18 cm
B. 12 cm
C. 9 3 cm
D. 6 3
Một chất điểm thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số. Nếu
hai dao động thành phần lệch pha nhau π 2 thì biên độ dao động tổng hợp là 20 cm. Nếu hai dao động thành phần ngược pha thì biên độ dao động tổng hợp là 15,6 cm. Biết biên độ của dao động thành phần thứ nhất lớn hơn so với biên độ của dao động thành phần thứ 2. Hỏi nếu hai dao động thành phần trên cùng pha với nhau thì biên độ dao động tổng hợp có giá trị gần giá trị nào nhất sau đây?
A. 21,2 cm.
B.27,5 cm.
C.23,9 cm.
D.25,4 cm.
Một chất điểm đồng thời tham gia hai dao động điều hòa cùng phương, cùng tần số, và cùng vị trí cân bằng. Biên độ và pha ban đầu của dao động thứ nhất lần lượt là A 1 = 4 cm và φ 1 = π/6. Biên độ và pha ban đầu của dao động thứ hai lần lượt là A 2 thay đổi được và φ 2 = -π/2. Thay đổi giá trị của A 2 để biên độ dao động tổng hợp có giá trị nhỏ nhất, giá trị đó bằng
A. 3 cm
B. 2 2 cm
C. 2 3 cm
D. 2 cm
Một chất điểm đồng thời tham gia hai dao động điều hòa cùng phương, cùng tần số, và cùng vị trí cân bằng. Biên độ và pha ban đầu của dao động thứ nhất lần lượt là A1 = 4 cm và φ1 = π/6. Biên độ và pha ban đầu của dao động thứ hai lần lượt là A2 thay đổi được và φ2 = -π/2. Thay đổi giá trị của A2 để biên độ dao động tổng hợp có giá trị nhỏ nhất, giá trị đó bằng
A. 3 cm
B. 2 cm
C. 2 2 cm
D. 2 3 cm
3. Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số với biên độ lần lượt là 4 cm và 10 cm. Tìm biên độ dao động tổng hợp khi
a. Hai dao động cùng pha
b. Hai dao động ngược pha nhau.
Một chất điểm thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số với biên độ lần lượt là A 1 và A 2 . Nếu hai dao động thành phần vuông pha nhau thì biên độ dao động tổng hợp là 20 cm. Nếu hai dao động thành phần ngược pha thì biên độ dao động tổng hợp là 15,6 cm. Hỏi nếu hai dao động thành phần cùng pha thì biên độ dao động tổng hợp có giá trị gần giá trị nào nhất sau đây ?
A. 24 cm.
B. 30 cm
C. 28 cm
D. 22 cm
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số. Dao động thứ nhất có biên độ bằng 6 cm và trễ pha với dao động tổng hợp π 2 rad. Khi dao động thứ hai có li độ bằng biên độ dao động thứ nhất thì dao động tổng hợp có li độ bằng 9 cm. Biên độ dao động tổng hợp nhận giá trị nào dưới đây?
A. 8 2 cm
B. 6 2 cm
C. 8 3 cm
D. 6 3 cm
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số. Biết dao động thứ nhất có biên độ A 1 = 6 cm và trễ pha 0,5π so với dao động tổng hợp. Tại thời điểm dao động thứ hai có li độ bằng biên độ của dao động thứ nhất thì dao động tổng hợp có li độ bằng 9 cm. Biên độ của dao động tổng hợp bằng
A. 18 cm
B. 12 cm
C. 9 3 cm
D. 6 3 cm