Trong tam giác ACD có góc ACD là góc tù .
Mà AD là cạnh đối diện với góc ACD.
⇒ AD là cạnh lớn nhất trong tam giác ACD (cạnh đối diện với góc tù là cạnh lớn nhất trong tam giác).
nên AD > AC hay AC < AD
Vậy Nếu : BC < BD thì AC < AD.
Trong tam giác ACD có góc ACD là góc tù .
Mà AD là cạnh đối diện với góc ACD.
⇒ AD là cạnh lớn nhất trong tam giác ACD (cạnh đối diện với góc tù là cạnh lớn nhất trong tam giác).
nên AD > AC hay AC < AD
Vậy Nếu : BC < BD thì AC < AD.
Một cách chứng minh khác của định lí 2:
Cho hình 13. Dùng quan hệ giữa góc và cạnh đối diện trong một tam giác để chứng minh rằng:
Nếu BC < BD thì AC < AD
Hướng dẫn:
Góc ACD là góc gì? Tại sao?
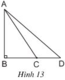
Cho tam giác ABD vuông tại B có C nằm Giữa B và D. Dùng quan hệ giữa góc và cạnh đối diện trong một tam giác để chứng minh: Nếu BC<BD thì AC<AD
1.Cho tam giác ABC có Â=90. Trên tia đối của tia AC lấy điểm D soa cho AD<AC. Nối B với D. Chứng minh: BC>BD(Chỉ sử dụng quan hệ giữa góc và cạnh đối diện)
2. Cho tam giác ABC. Chứng minh rằng AB+AC>BC(sử dụng qh giữa góc và cạnh đối diện)
3.Cho tam giác ABC(AB=AC), D là điểm bất kì trong tam giác sao cho ADB>ADC. Chứng minh rằng DC>DB(sd qh giữa góc và cạnh đối diện)
mik cần gấp, ai đúng và nhanh mik sẽ tick!!!
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường vuông góc AH đến đường thẳng BC (H thuộc BC).
Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở Bài 1 để chứng minh AB + AC > BC.
cho tam giác abc nhọn có AB<AC . Tia phân giác góc A cắt BC tại D . Chứng minh rằng DB<DC ( bài này là quan hệ giữa góc và cạnh đối diện trong 1 tam giác nha)
Một cách chứng minh khác của bất đẳng thức:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường thẳng vuông góc AH đến đường thẳng BC.
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông để chứng minh AB+ AC> BC.
b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại.
Chứng minh định lí : Nếu 2 tam giác có 2 cặp cạnh tương ứng = nhau, góc xen giữa khác nhau, cạnh đối diện vs góc lớn hơn thì lớn hơn
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. kẻ đường vuông góc AH đến đường thẳng BC (H ε BC)
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông để chứng minh AB + AC > BC
b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại
Cho tam giác ABC, AB < AC và AD là tia phân giác của góc A (D\(\in\)BC) .Kẻ AH\(⊥\)BC. M là trung điểm của cạnh BC.CMR: Tia AD nằm giữa AH và AM. giải chi tiết cho mình nha,mình mới tích(gợi ý: dùng quan hệ giữa góc và cạnh đối diện trong tam giác, định lí là:tam giác ABC có AB=DE,góc A < góc D,AC=DF thì BC<EF hoặc ngược lại)