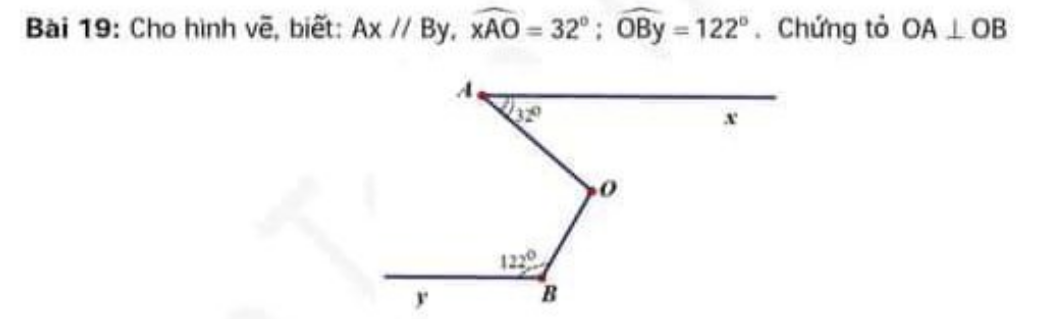
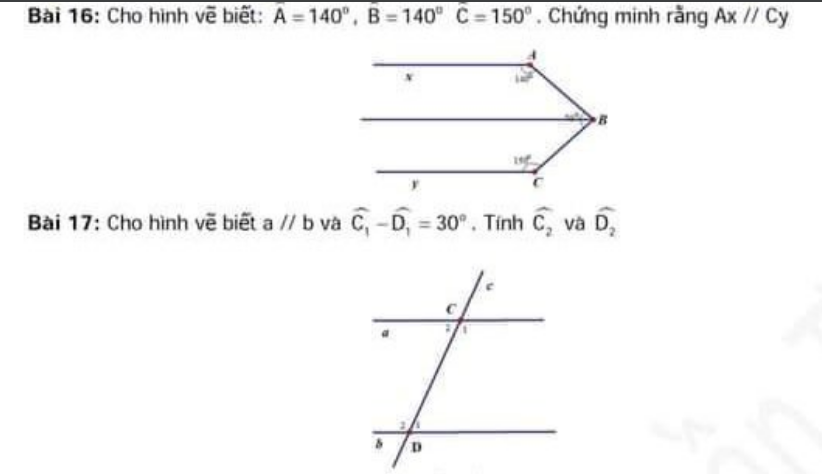
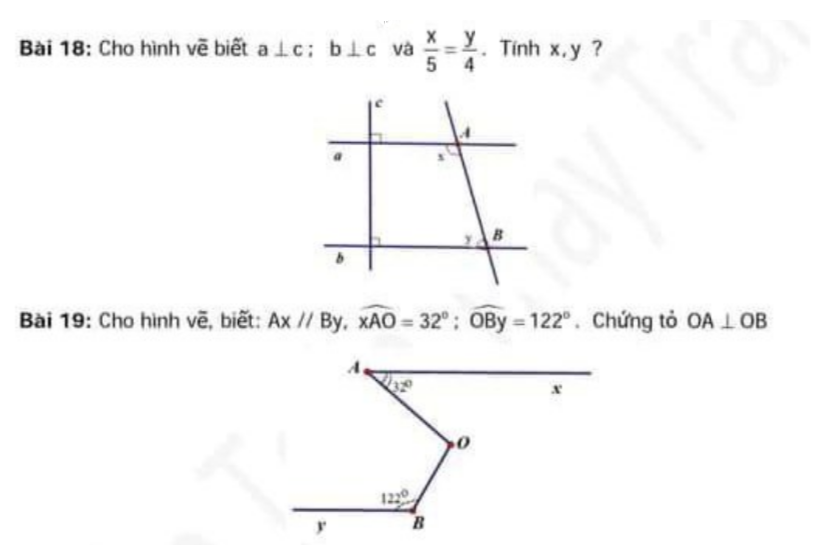
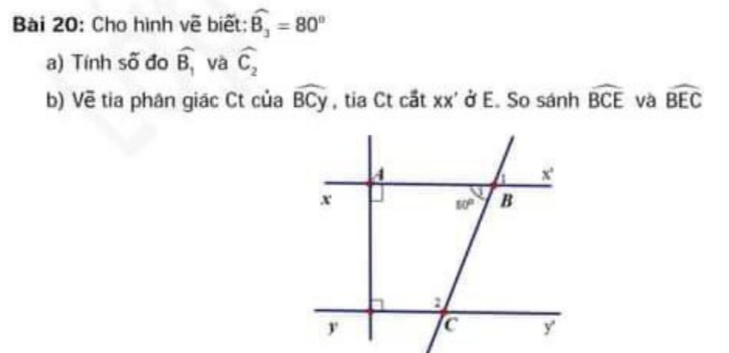
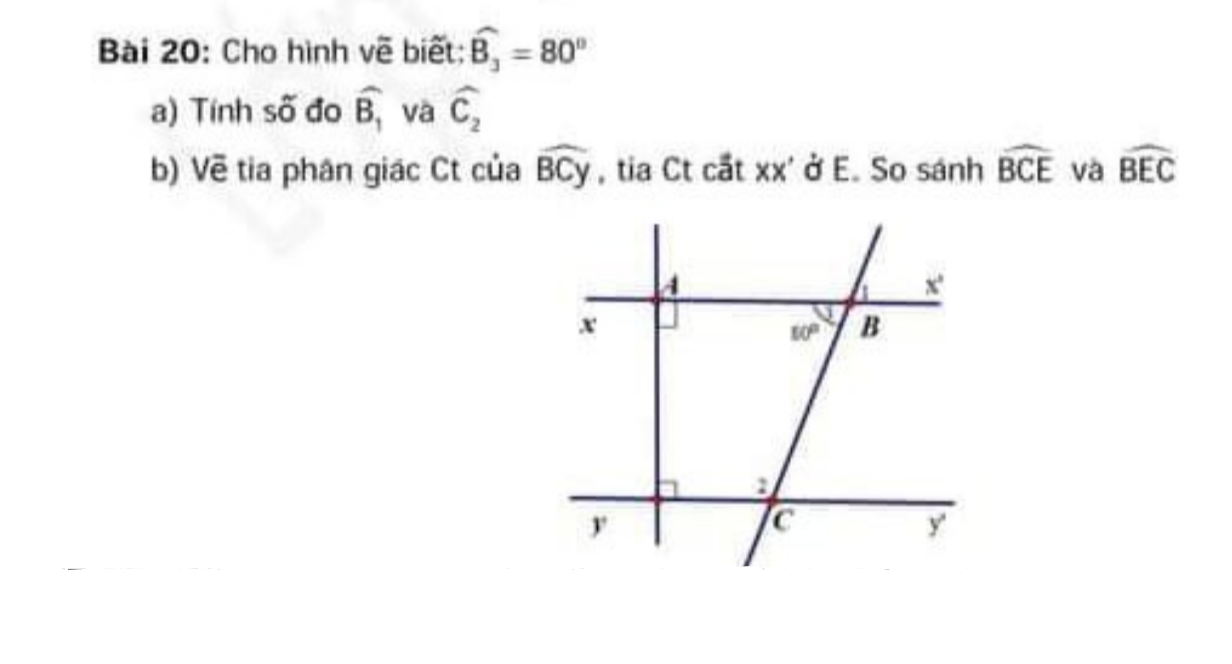
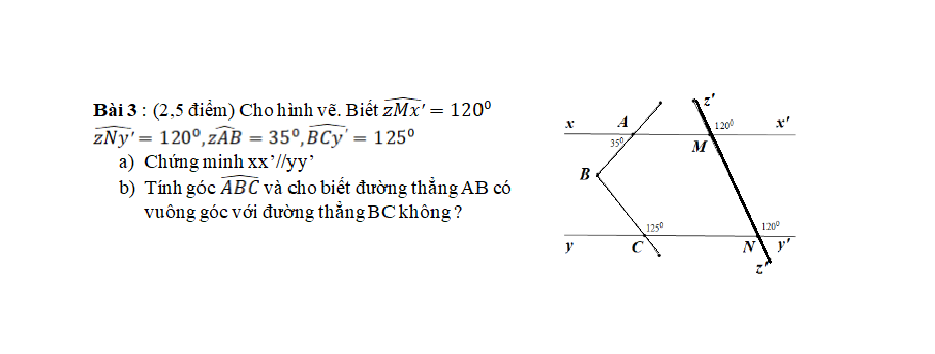B1 dùng đối đỉnh c2 dùng tổng các góc bằng 360° gì đấy
a)
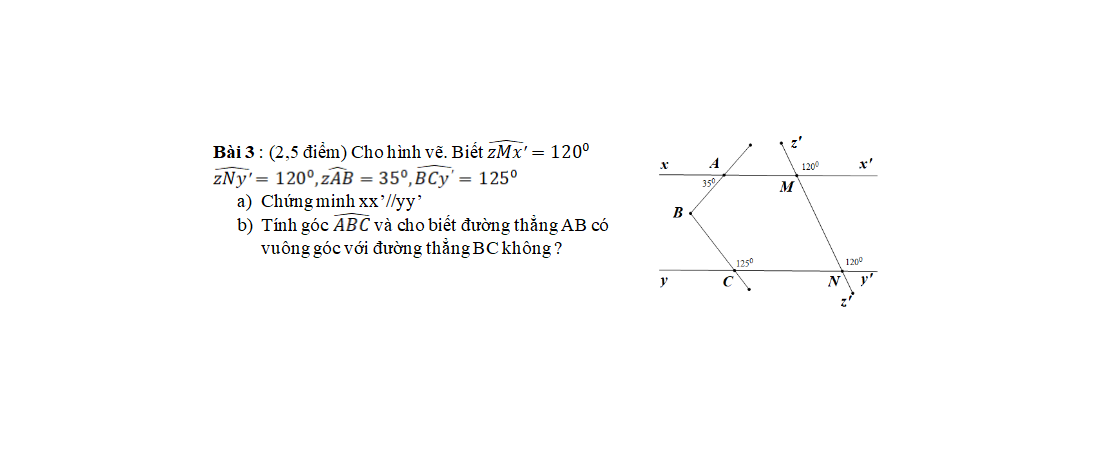
+ Ta có: \(\widehat{B_3}\)= 80o ( Theo đề bài)
⇒\(\widehat{B_1}=\widehat{B_3}=80^o\) (Đối đỉnh)
+Vì \(\widehat{B_3}\) và \(\widehat{C_2}\) ở vị trí trong cùng phía nên ta có:
\(\widehat{B_3}+\widehat{C_2}=180^o\)
Hay 80\(^o\)+\(\widehat{C_2}\)= 180\(^o\)
⇒ \(\widehat{C_2}=180^o-80^o\)
⇒ \(\widehat{C_2}=100^o\)
b)
+Ta có: \(\widehat{C_2}+\widehat{BCy'}=180^o\) (Kề bù)
Hay \(100^o+\widehat{BCy'}=180^o\)
⇒ \(\widehat{BCy'}=180^o-100^o\)
\(\widehat{BCy'}=80^o\)
+Vì Ct là tia phân giác của \(\widehat{BCy'}\) nên ta có:
\(\widehat{BCE}=\widehat{ECy'}=\dfrac{1}{2}\widehat{BCy'=\dfrac{1}{2}.}\)\(80^o\)= \(40^o\)
+Qua E kẻ tia m, m // CB
Ta có: \(\widehat{ABC}=\widehat{BEm}=80^o\) (Đồng vị)
⇒\(\widehat{BEC}=80^o-40^o=40^o\)
⇒\(\widehat{BCE}=\widehat{BEC}\)