Bài 3:
a. $[25+(-15)]+(-25)=25-15-25=(25-25)-15=0-15=-15$
b. $512-(-88)-400-112$
$=512+88-400-112$
$=(512-112-400)+88=(400-400)+88=88$
c.
$-(310)+(-290)-907+107=-310-290-907+107$
$=-(310+290)-(907-107)=-600-600=-1200$
d.
$-2004-1975+2000-2025$
$=-(2004-2000)-(1975+2025)=-4-4000=-(4+4000)=-4004$
Bài 1:
a. $ax+ay+bx+by=(ax+ay)+(bx+by)=a(x+y)+b(x+y)$
$=(x+y)(a+b)=17(-2)=-34$
b. $ax-ay+bx-by = (ax-ay)+(bx-by)$
$=a(x-y)+b(x-y)=(x-y)(a+b)=(-1)(-7)=7$
Bài 2:
a. Bội của 1 số $k$ tự nhiên nào đó có dạng $nk$ với $n$ là số tự nhiên bất kỳ, như $0, k, 2k, 3k,4k,...$
Tương tự vậy thì bội của $5$ có dạng $5n$ với $n$ là số tự nhiên bất kỳ
b.
Tất cả các số chẵn có dạng $2k$ với $k$ là số nguyên nào đó
c. Tất cả các số lẻ có dạng $2k+1$ với $k$ là số nguyên nào đó.
Bài 4:
Gọi số cần tìm là $\overline{ab}$ với $a,b$ là stn có 1 chữ số, $a\neq 0$
Theo bài ra ta có:
$\overline{ab}=5(a+b)$
$\Rightarrow 10a+b=5a+5b$
$5a=4b$
Vì $a\neq 0$ nên $b\neq 0$. Vì $4b=5a\vdots 5$ nên $b\vdots 5$
Mà $b\neq 0$, $b\leq 9$ nên $b=5$
$\Rightarrow a=4$
Vậy số cần tìm là $45$
Bài 5:
a. Ta có:
$10^{28}=2^{28}.5^{28}=2^3.2^{25}.5^{28}=8.2^{25}.5^{28}\vdots 8$
$8\vdots 8$
$\Rightarrow 10^{28}+8\vdots 8(1)$
Mặt khác:
Gọi $B(n)$ là bội số của số $n$. Chỉ cần là bội của n thì ký hiệu như vậy, bất kể số nào.
$10^{28}+8=(9+1)^{28}+8=B(9)+1+8=B(9)+9=B(9)$
$\Rightarrow 10^{28}+8\vdots 9(2)$
Từ $(1); (2)$ kết hợp với $(8,9)=1$ nên $\Rightarrow 10^{28}+8\vdots (8.9)$ hay $10^{28}+8$ chia hết cho $72$
b.
$8^{8}+2^{20}=2^{24}+2^{20}=2^{20}(2^4+1)=2^{20}.17\vdots 17$ (đpcm)
c.
$81^7-27^9-9^{13}=(3^4)^7-(3^3)^9-(3^2)^{13}=3^{28}-3^{27}-3^{26}$
$=3^{26}(3^2-3-1)=3^{26}.5=3^{24}.3^2.5=45.3^{24}\vdots 45$
d.
$10^9+10^8+10^7=10^7(10^2+10+1)$
$=10^7.111=10^6.2.5.111=555.2.10^6\vdots 555$ (đpcm)






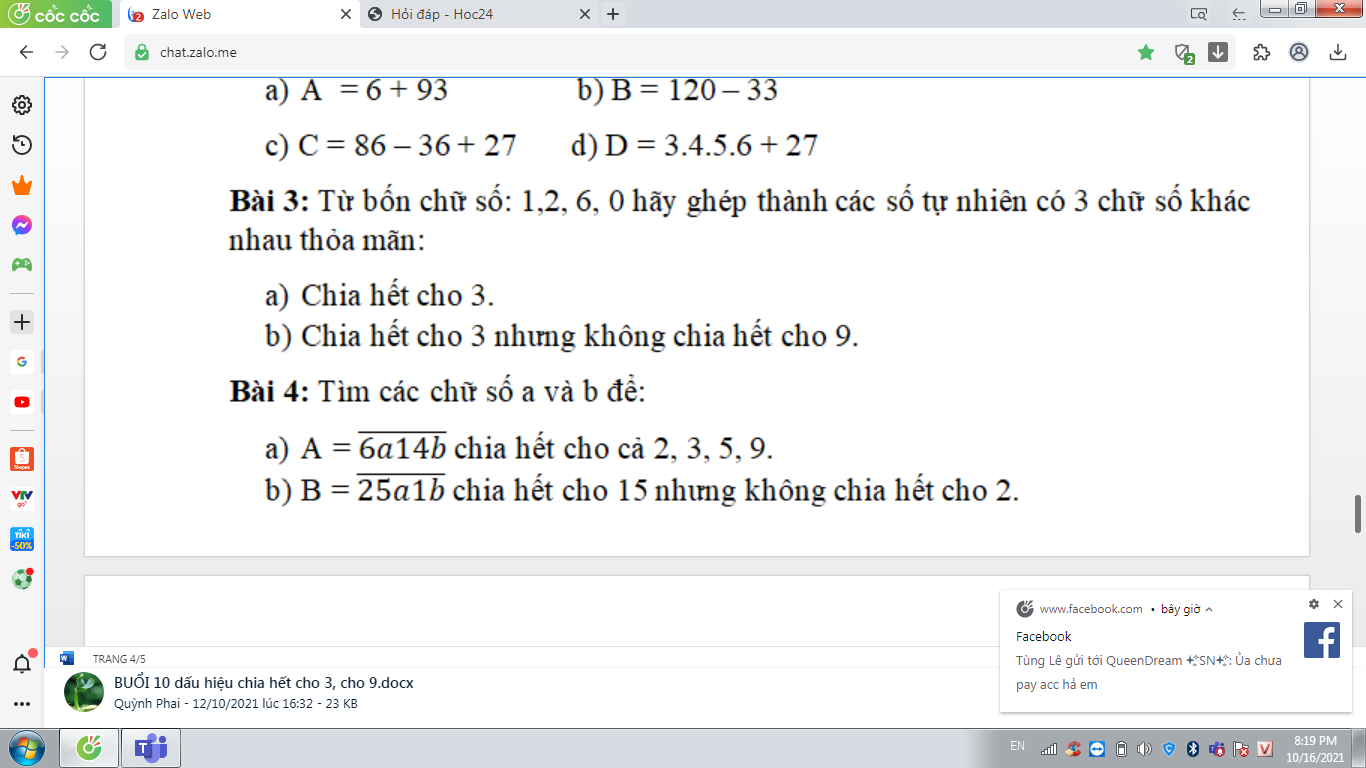 mọi người làm cho em bài 4 với ạ em đang cần gấp lắm
mọi người làm cho em bài 4 với ạ em đang cần gấp lắm


 Mọi người ơi giúp 2 bài giải có lời giải chi tiết đi ạ ảnh dưới là cách làm mẫu làm ơn giúp mình vì mình đang cần gấp!
Mọi người ơi giúp 2 bài giải có lời giải chi tiết đi ạ ảnh dưới là cách làm mẫu làm ơn giúp mình vì mình đang cần gấp!




