\(\Rightarrow\dfrac{3}{4}\cdot\dfrac{9}{22}-\left|-3x+\dfrac{8}{3}\right|=\dfrac{3}{4}\\ \Rightarrow\left|-3x+\dfrac{8}{3}\right|=\dfrac{11}{6}-\dfrac{3}{4}=\dfrac{13}{12}\\ \Rightarrow\left[{}\begin{matrix}-3x+\dfrac{8}{3}=\dfrac{13}{12}\\3x-\dfrac{8}{3}=\dfrac{13}{12}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}3x=\dfrac{19}{12}\\3x=\dfrac{15}{4}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{19}{36}\\x=\dfrac{5}{4}\end{matrix}\right.\)
\(\dfrac{3}{4}:2\dfrac{4}{9}-\left|-3x+2\dfrac{2}{3}\right|=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{3}{4}:\dfrac{22}{9}-\left|-3x+\dfrac{8}{3}\right|=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{27}{88}-\left|-3x+\dfrac{8}{3}\right|=\dfrac{3}{4}\)
\(\Rightarrow\left|-3x+\dfrac{8}{3}\right|=-\dfrac{39}{88}\left(VLý\right)\)
Vậy \(S=\varnothing\)


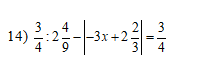 mọi người ơi giúp mình câu này với mình hứa sẽ kích đúng
mọi người ơi giúp mình câu này với mình hứa sẽ kích đúng