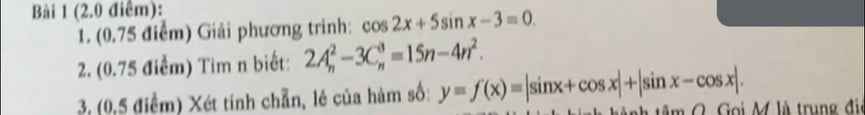1.1
\(cos2x+5sinx-3=0\)
\(\Leftrightarrow1-2sin^2x+5sinx-3=0\)
\(\Leftrightarrow2sin^2x-5sinx+2=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx=2\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
1.2
\(2A^2_n-3C^3_n=15n-4n^2\)
\(\Leftrightarrow2\dfrac{n!}{\left(n-2\right)!}-3\dfrac{n!}{\left(n-3\right)!.3!}=15n-4n^2\)
\(\Leftrightarrow2n\left(n-1\right)-\dfrac{n\left(n-1\right)\left(n-2\right)}{2}=15n-4n^2\)
\(\Leftrightarrow4n^2-4n-n^3+3n^2-2n=30n-8n^2\)
\(\Leftrightarrow n^3-15n^2+36n=0\)
\(\Leftrightarrow\left[{}\begin{matrix}n=0\left(l\right)\\n=3\left(tm\right)\\n=12\left(tm\right)\end{matrix}\right.\)
1.3
\(f\left(-x\right)=\left|-sinx+cosx\right|+\left|-sinx-cosx\right|=\left|sinx+cosx\right|+\left|sinx-cosx\right|=f\left(x\right)\)
\(\Rightarrow\) Là hàm số chẵn
\(-f\left(x\right)=-\left|sinx+cosx\right|-\left|sinx-cosx\right|\ne f\left(-x\right)\)
\(\Rightarrow\) Không phải hàm số lẻ
25.
Phương trình đã cho có nghiệm khi:
\(m^2+9m^2\ge49\Leftrightarrow10m^2\ge49\Leftrightarrow\left[{}\begin{matrix}m\ge\dfrac{7}{\sqrt{10}}\\m\le-\dfrac{7}{\sqrt{10}}\end{matrix}\right.\)
26.
\(2cosx-\sqrt{3}=0\)
\(\Leftrightarrow cosx=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+k2\pi\)
TH1: \(x=\dfrac{\pi}{6}+k2\pi\Rightarrow\) Nghiệm âm lớn nhất và nghiệm dương nhỏ nhất là \(-\dfrac{11\pi}{6};\dfrac{\pi}{6}\)
TH2: \(x=-\dfrac{\pi}{6}+k2\pi\Rightarrow\) Nghiệm âm lớn nhất và nghiệm dương nhỏ nhất là \(-\dfrac{\pi}{6};\dfrac{11\pi}{6}\)
Vậy tổng \(S=-\dfrac{\pi}{6}+\dfrac{\pi}{6}=0\)