`(x + 1)(x - 3 ) - x^2 = 2 ( x - 2 )`
`<=>x^2 - 3x + x - 3 - x^2 = 2x - 4`
`<=> x^2 - x^2 - 3x + x - 2x = - 4 + 3`
`<=> -4x = -1`
`<=> x = 1 / 4`
Vậy `S = { 1 / 4 }`
Bổ sung `b` và `c`
`b) 3 / [ x + 3 ] + x / [ x - 3 ] = 1` `ĐK: x \ne +-3`
`<=> [ 3 ( x - 3 ) + x ( x + 3 ) ] / [ ( x - 3 ) ( x + 3 ) ] = [ ( x - 3 ) ( x + 3 ) ] / [ ( x - 3 ) ( x + 3 ) ]`
`=> 3x - 9 + x^2 + 3x = x^2 - 9`
`<=> x^2 - x^2 + 3x + 3x = -9 + 9`
`<=> 6x = 0`
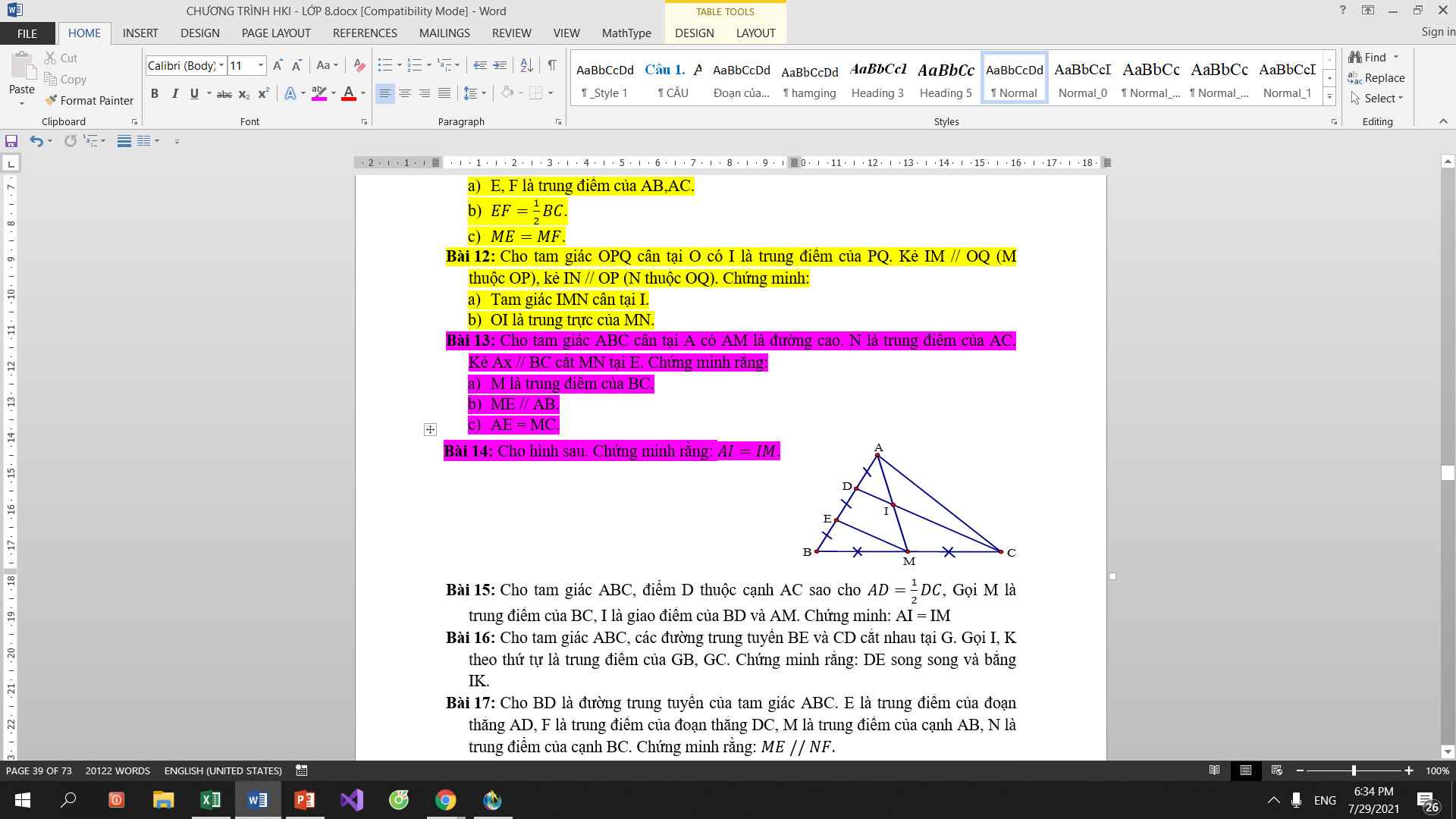
`<=> x = 0` (t/m)
Vậy `S = { 0 }`
___________________________________________
`c) | x + 7 | = 3x + 1`
`@TH1: x + 7 >= 0 <=> x >= -7`
`=> | x + 7 | = x + 7`
`=> x + 7 = 3x + 1`
`<=> 2x = 6`
`<=> x = 3` (t/m)
`@TH2: x + 7 < 0 <=> x < -7`
`=> | x + 7 | = -x - 7`
`=> - x - 7 = 3x + 1`
`<=> 4x = -8`
`<=> x = -2` (ko t/m)
Vậy `S = {3}`
a.\(\left(x+1\right)\left(x-3\right)-x^2=2\left(x-2\right)\)
\(\Leftrightarrow x^2-3x+x-3-x^2=2x-4\)
\(\Leftrightarrow-4x=-1\)
\(\Leftrightarrow x=\dfrac{1}{4}\)
b.\(\dfrac{3}{x+3}+\dfrac{x}{x-3}=1\) ;\(ĐK:x\ne\pm3\)
\(\Leftrightarrow\dfrac{3\left(x-3\right)+x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
\(\Leftrightarrow3\left(x-3\right)+x\left(x+3\right)=\left(x-3\right)\left(x+3\right)\)
\(\Leftrightarrow3x-9+x^2+3x=x^2-9\)
\(\Leftrightarrow6x=0\)
\(\Leftrightarrow x=0\left(tm\right)\)
c.\(\left|x+7\right|=3x+1\)
\(\Leftrightarrow\left[{}\begin{matrix}x+7=3x+1;x\ge-7\\-x-7=3x+1;x< 7\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-2\left(tm\right)\end{matrix}\right.\)