mọi người giúp em với ạ
em cảm ơn mọi người rất nhiều ạ
Bài 5. Cho tam giác \(ABC\) vuông tại \(A\), kẻ phân giác \(BD\) của góc \(ABC\) (\(D\) thuộc \(AC\)), kẻ \(AH \perp BD (H \in BD)\), \(AH\) cắt \(BC\) tại \(E\).
a) \(\triangle ABH = \triangle EBH\)
b) Chứng minh: \(DE \perp BC\). Từ đó chứng minh \(AD < DC\)
c) Gọi \(F\) là giao điểm của \(AB\) và \(DE\). So sánh \(EF\) và \(AF\)
d) Kẻ \(AK\) vuông góc với \(BC\) (\(K \in BC\)). Chứng minh: \(AE\) là tia phân giác của \(\angle CAK\).
a.
Xét hai tam giác ABH và EBH có:
\(\widehat{ABH}=\widehat{EBH}\) (do AD là phân giác)
`BH` là cạnh chung
\(\widehat{BHA}=\widehat{BHE}=90^0\) (do \(AE\perp BD\))
\(\Rightarrow\Delta ABH=\Delta EBH\left(g.c.g\right)\)
b.
Từ câu a, do \(\Delta ABH=\Delta EBH\) suy ra \(BA=BE\)
Xét hai tam giác BAD và BED có:
\(BA=BE\) (cmt)
\(\widehat{ABD}=\widehat{EBD}\) (do AD là phân giác)
`BD` là cạnh chung
\(\Rightarrow\Delta BAD=\Delta BED\left(c.g.c\right)\) (1)
\(\Rightarrow\widehat{BED}=\widehat{BAD}\)
Mà tam giác ABC vuông tại A nên \(\widehat{BAD}=90^0\)
\(\Rightarrow\widehat{BED}=90^0\Rightarrow DE\perp BC\)
Từ (1) suy ra `AD=DE` (2)
Do \(DE\perp BC\) nên tam giác CDE vuông tại E
\(\Rightarrow DE< DC\) (quan hệ giữa cạnh huyền và cạnh góc vuông) (3)
Từ (2) và (3) \(\Rightarrow AD< DC\)
c.
Xét tam giác AEF, ta có \(\widehat{EAF}=\widehat{EAC}+\widehat{CAF}\)
\(\Rightarrow\widehat{EAF}=\widehat{EAC}+90^0\)
\(\Rightarrow\widehat{EAF}>90^0\)
\(\Rightarrow\widehat{EAF}\) là góc tù nên là góc lớn nhất trong tam giác AEF
\(\Rightarrow\widehat{EAF}>\widehat{AEF}\)
\(\Rightarrow EF>AF\) (quan hệ giữa cạnh và góc trong tam giác)
d.
Theo cm câu b, do \(\Delta BAD=\Delta BED\Rightarrow AD=ED\)
\(\Rightarrow\Delta ADE\) cân tại D
\(\Rightarrow\widehat{DAE}=\widehat{DEA}\) (4)
Mặt khác do \(AK\perp BC\Rightarrow AK||DE\) (cùng vuông góc BC)
\(\Rightarrow\widehat{KAE}=\widehat{DEA}\) (hai góc so le trong) (5)
Từ (4) và (5) \(\Rightarrow\widehat{KAE}=\widehat{DAE}\)
\(\Rightarrow AE\) là tia phân giác của \(\widehat{CAK}\)
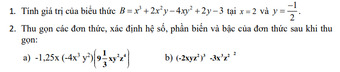
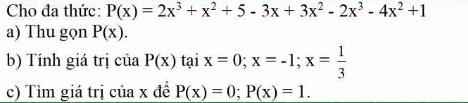
mng giúp em với ạ.Em rất cảm ơn mọi người ạ
