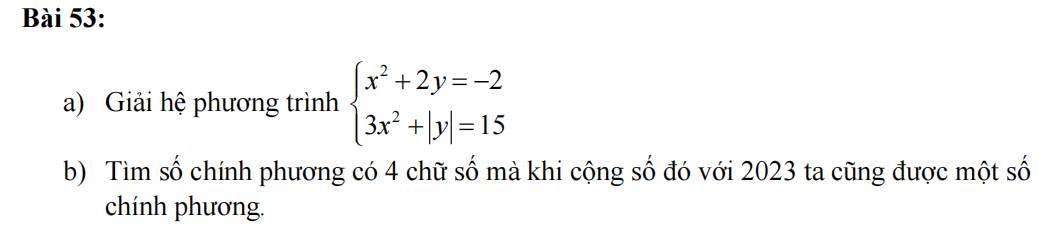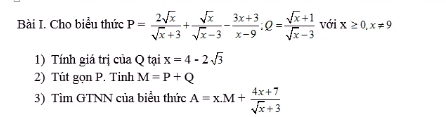a.
- Với \(y\ge0\Rightarrow x^2+2y\ge0\) với mọi x \(\Rightarrow\) hệ vô nghiệm do \(-2< 0\)
- Với \(y< 0\Rightarrow\left|y\right|=-y\), hệ tương đương:
\(\left\{{}\begin{matrix}x^2+2y=-2\\3x^2-y=15\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^2+2y=-2\\6x^2-2y=30\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+2y=-2\\7x^2=28\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^2=4\\y=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\pm2\\y=-3\end{matrix}\right.\)
b.
Gọi số chính phương cần tìm là \(n^2\) với n là số tự nhiên, do \(n^2\) có 4 chữ số
\(\Rightarrow999< n^2< 10000\Rightarrow31< n< 100\)
Do khi cộng số cần tìm với 2023 ta cũng được 1 SCP
\(\Rightarrow n^2+2023=m^2\) (với m tự nhiên và \(m>n\))
\(\Rightarrow m^2-n^2=2023\)
\(\Rightarrow\left(m-n\right)\left(m+n\right)=2023\)
Ta chỉ cần xét các cặp ước của 2023 mà \(m+n>m-n\)
| m-n | 1 | 7 | 17 |
| m+n | 2023 | 289 | 119 |
| m | 1012 | 148 | 68 |
| n | 1011 | 141 | 51 |
Do \(31< n< 100\) nên chỉ có \(n=51\) thỏa mãn
Vậy số cần tìm là \(51^2=2601\)