Lời giải:
$x^2+\frac{1}{x^2}=7$
$\Leftrightarrow (x+\frac{1}{x})^2=9\Rightarrow x+\frac{1}{x}=3$ hoặc $x+\frac{1}{x}=-3$
$A=x^7+\frac{1}{x^7}=(x^3+\frac{1}{x^3})(x^4+\frac{1}{x^4})-(x+\frac{1}{x})$
Trong đó:
$x^3+\frac{1}{x^3}=(x+\frac{1}{x})^3-3x.\frac{1}{x}(x+\frac{1}{x})=(x+\frac{1}{x})^3-3(x+\frac{1}{x})$
$x^4+\frac{1}{x^4}=(x^2+\frac{1}{x^2})^2-2$
$=[(x+\frac{1}{x})-2]^2-2$
Ta biết giá trị của $x+\frac{1}{x}$ rồi thì chỉ cần thay vào tính A thôi.












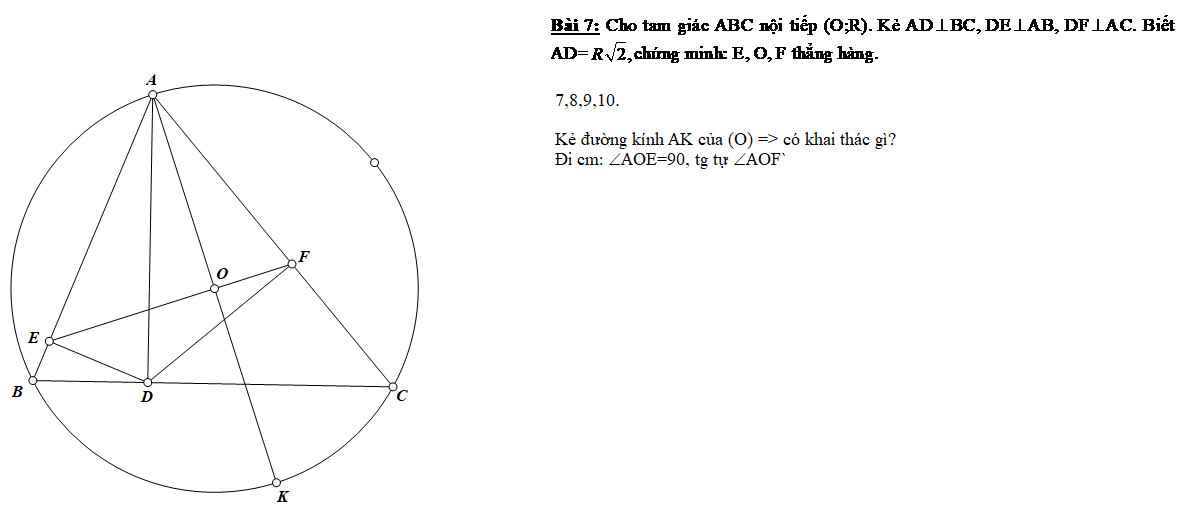



 em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ




