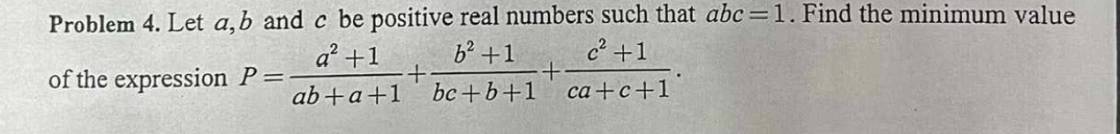Với mọi a;b;c ta có:
\(\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge2\left(a+b+c\right)-3\) (1)
Đồng thời cũng có:
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)
\(\Leftrightarrow6\left(a^2+b^2+c^2\right)\ge6\left(ab+bc+ca\right)\) (2)
Cộng vế (1) và (2):
\(\Rightarrow7\left(a^2+b^2+c^2\right)\ge2\left(a+b+c\right)+6\left(ab+bc+ca\right)-3\)
\(\Leftrightarrow7\left(a^2+b^2+c^2\right)\ge2\left(a+b+c+3ab+3bc+3ca\right)-3=21\)
\(\Rightarrow a^2+b^2+c^2\ge3\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)

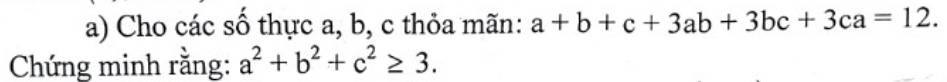












 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ