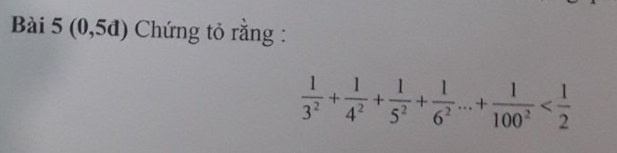\(\Leftrightarrow\dfrac{1}{3^2}+\dfrac{1}{4^2}+....+\dfrac{1}{100^2}< \dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\\ \Leftrightarrow Ta.thay:\\ \dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3};\dfrac{1}{3.4}=\dfrac{1}{3}-\dfrac{1}{4};...;\dfrac{1}{99.100}=\dfrac{1}{99}-\dfrac{1}{100}\\ \Leftrightarrow A< \dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ \Leftrightarrow A< \dfrac{1}{2}-\dfrac{1}{100}< \dfrac{1}{2}\\ \Rightarrow A< \dfrac{1}{2}\\ \Rightarrow\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< \dfrac{1}{2}\left(đpcm\right)\)
Đúng 4
Bình luận (2)
Các câu hỏi tương tự
Tìm x thuộc Z, biết:
|x+19|+|x+5|+|x+2020|=5x
Mọi người giải chi tiết giúp em với ạ!
Mọi người giúp mình bài này với. Các bạn cho mình lời giải chi tiết nha. Mình cảm ơn^^
Tìm x:
\(\dfrac{x-2}{5}\)=\(\dfrac{1-x}{6}\)
Mọi người giải chi tiết giúp e với ạ. E cảm ơn!
(1+1/2).(1+1/3).(1+1/4)...(1+1/99)
GIẢI CHI TIẾT GIÚP MÌNH VỚI Ạ. CẢM ƠN MỌI NGƯỜI!
Tìm x 1+2+3+...+x=5050
Mình cần cách giải chi tiết
Mọi người giúp mình với!
Cho a<b, c<d. Hãy so sánh a+c và b+d.
Mọi người giúp mình với ạ, mình đang cần gấp. ( phiền mọi người giải chi tiết luôn nhé!)
Dựa vào đồng dư thức, hãy tìm số dư của:
3^100 + 3^105 khi chia cho 13
( Giải chi tiết giúp em nha mọi người)
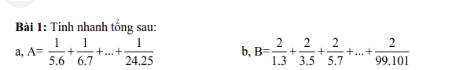
giúp em với ạ ( giải chi tiết giúp em ạ)
Mọi người giải chi tiết giúp em với ạ
Tính giá trị biểu thức
a, A=(100-1) . (100-2) . (100-3) .... (100-n) với n thuộc N* và tích trên có đúng 100 thừa số
b, B=13a +19b +4a -2b với a+b=100