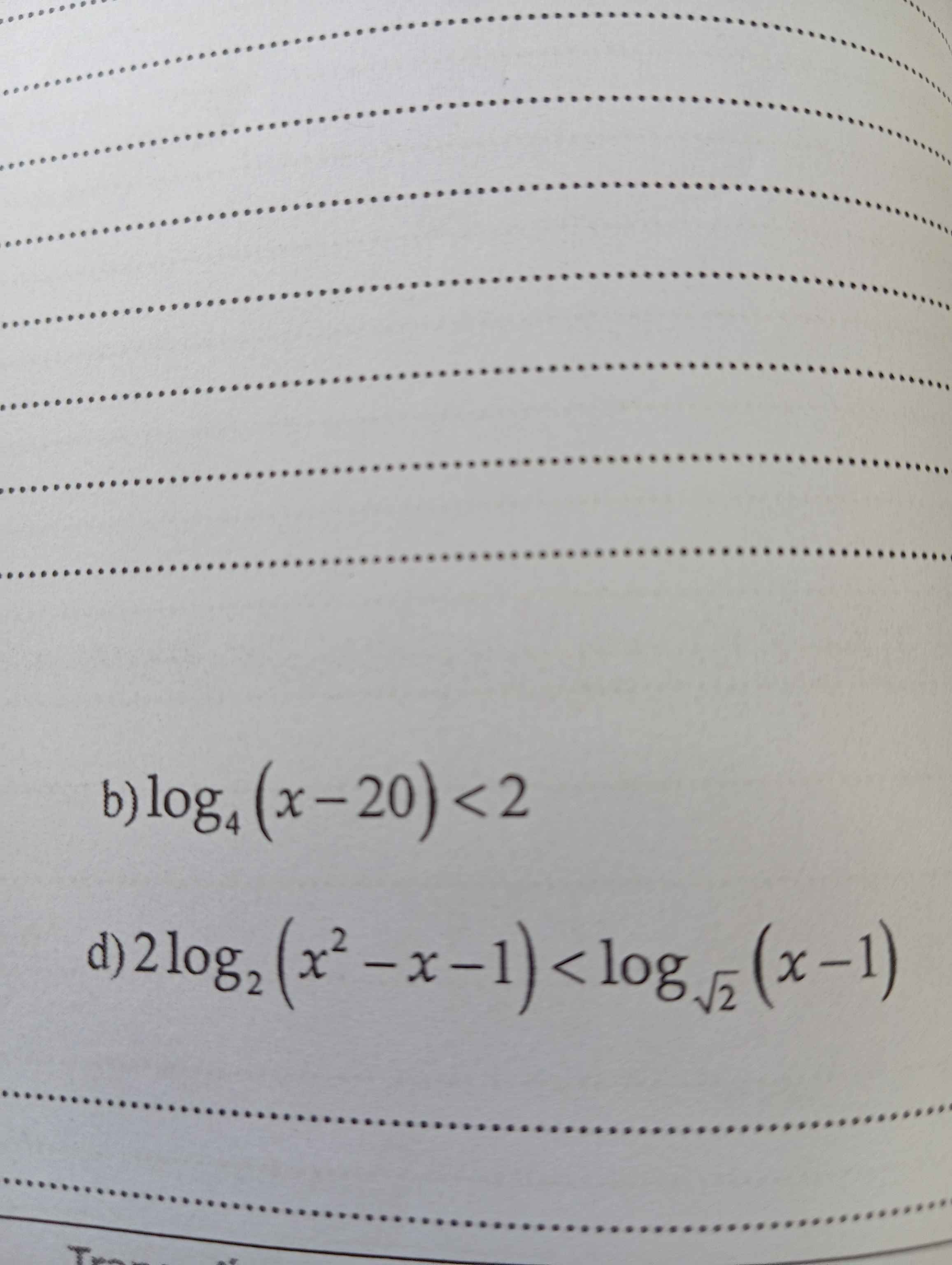\(b) log_{4}(x-20)<2\)
ĐKXĐ: \(x-20 > 0 => x > 20\)
\(4^2 > x-20\) ( Định lí logarit)
\(16 > x-20\)
\(x < 36 \)
=> Nghiệm của bất phương trình là 20 < x < 36
d.\(2log_2\left(x^2-x-1\right)< log_{\sqrt{2}}\left(x-1\right)\)
ĐKXĐ: \(x^2-x-1 > 0\)
\(x-1 > 0 => x > 1\)
\( x^2-x-1 > 0\)
-> \(x < \frac{1-\sqrt{5}}{2}\) hoặc \(x > \frac{1+\sqrt{5}}{2}.\)
Với điều kiện x > 1, ta có điều kiện xác định chung là \(x > \frac{1+\sqrt{5}}{2}\)
Ta có:
\(2log_{2}(x^2-x-1) = log_{2}(x^2-x-1)^2\)
\(log_{\sqrt{2}}(x-1) = log_{2^{1/2}}(x-1) = 2log_{2}(x-1) \)
\(log_{2}(x^2-x-1)^2 < 2log_{2}(x-1)\)
\(log_{2}(x^2-x-1)^2 < log_{2}(x-1)^2 \)
\((x^2-x-1)^2 < (x-1)^2\)
\(x^4 - 2x^3 - x^2 + 2x + 1 < x^2 - 2x + 1\)
\(x^4 - 2x^3 - 2x^2 + 4x < 0\)
\(x(x-2)(x^2-4) < 0 \)
\(x(x-2)(x-2)(x+2) < 0\)
\(x(x-2)^2(x+2) < 0\)
Bất phương trình này có nghiệm là -2 < x < 0 hoặc 0 < x < 2
Với điều kiện xác định \(x > \frac{1+\sqrt{5}}{2}\), nghiệm của bất phương trình là \(\frac{1+\sqrt{5}}{2} < x < 2\)