Bài 1:
Áp dụng BĐT Bunhiacopxky:
$(4x^2+y^2)(1+1)\geq (2x+y)^2$
$\Rightarrow \frac{4x^2+y^2}{2}\geq (\frac{2x+y}{2})^2$
$\Rightarrow \sqrt{\frac{4x^2+y^2}{2}}\geq \frac{2x+y}{2}(*)$
Và:
$4(4x^2+2xy+y^2)=[3x^2+(x+y)^2](1+3)\geq [\sqrt{3}x+\sqrt{3}(x+y)]^2$
$\Rightarrow 4(4x^2+2xy+y^2)\geq 3(2x+y)^2$
$\Rightarrow \sqrt{\frac{4x^2+2xy+y^2}{3}}\geq \frac{2x+y}{2}(**)$
Từ $(*); (**)\Rightarrow \text{VT}\geq 2x+y$ (đpcm)
Dấu "=" xảy ra khi $x=\frac{y}{2}>0$
Bài 2:
Tìm min:
Vì $x\geq 4; y\geq 9$ nên hiển nhiên $A\geq 0$
$\Rightarrow A_{\min}=0$. Dấu "=" xảy ra khi $y=9; x=4$
----------
Tìm max:
Áp dụng BĐT AM-GM
\(A=\frac{\sqrt{y-9}}{y}+\frac{\sqrt{x-4}}{x}\leq \frac{\frac{(y-9)+9}{6}}{y}+\frac{\frac{(x-4)+4}{4}}{x}=\frac{1}{6}+\frac{1}{4}=\frac{5}{12}\)
Vậy $A_{\max}=\frac{5}{12}$


















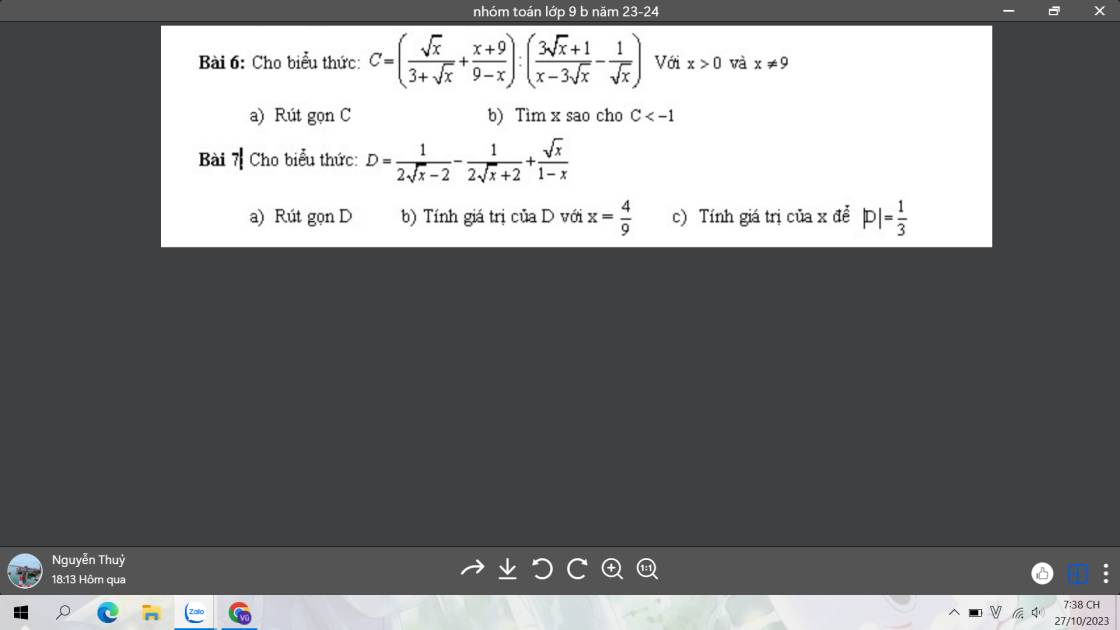 giúp mik với mn ơi mik đg cần gấp
giúp mik với mn ơi mik đg cần gấp

