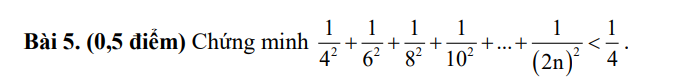\(\Rightarrow A=\dfrac{1}{\left(2\cdot2\right)^2}+\dfrac{1}{\left(2\cdot3\right)^2}+\dfrac{1}{\left(2\cdot4\right)^2}+...+\dfrac{1}{\left(2n\right)^2}\\ A=\dfrac{1}{4}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{n^2}\right)< \dfrac{1}{4}\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{\left(n-1\right)n}\right)\\ A< \dfrac{1}{4}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{\left(n-1\right)}-\dfrac{1}{n}\right)\\ A< \dfrac{1}{4}\left(1-\dfrac{1}{n}\right)< \dfrac{1}{4}\left(\text{đ}pcm\right)\)
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
mn người ơi giúp mik với
cảm ơn mn rất nhìu
![]()
mn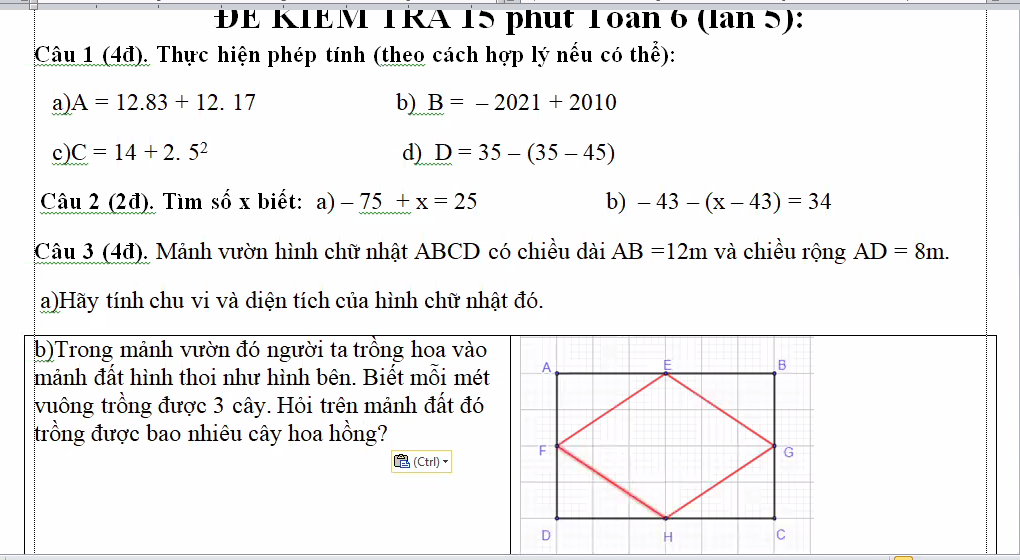
mn người ơi giúp mik với,cảm ơn mn rất nhìu mn ! 
Mn ơi helpppp!!!!!!!!!!!! Giúp mikk với mn ơiiiiii ! Please giúp mikkk nhennn! Làm ơn huhuuuuu giúp mikk! Thanks kiu mn rất rấttt nhìu nhìu nhìuuuu lunnnn! Mỗi ng làm 1 bài giúp mik với!

Bài 2 : Tìm số nguyên x , biết
a) (-2) . ( x+7 ) + (-5) = 7
b)(x+4) : (-7) = 14
c) 72 : ( x+5) - 4 = -12
d) (x+3) : (-6 ) + 12 = 8
mn ơi giúp mik với zới mik thật sự cần rất gấp bài này mong mn sẽ giúp mik , cảm ơn mn nhìu
Mong mn giúp mik với ạ. Cảm ơn rất nhìu !!!
A=3/1.4+3/4.7+3/7.10+.....+3/3001.3004
Tính A
Tính nhanh
23 x 58 - 30 x 23 + 28 x 77 =
giúp mik zới mn ui , mik cần gấp lắm , làm ơn giúp mình ik mà mn , năn nỉ mn đó , giải tích cả cahs làm cho mik nhé , thank you mn nhìu ạ , kết quả gợi ý là 2800 mik mong các bạn sẽ trả lời đúng kết quả mà mik gợi ý , mong mn sẽ giúp mik , cảm ơn mn nhìu ạ

mn giải giúp mình vs
mình cảm ơn rất nhìu
Bài 4 : Có 20 quả cam ; 30 hộp bánh và 45 gói kẹo . Cô giáo muốn chia đều số cam vào các đĩa , số hộp bánh và số gói kẹo cúng vậy . Hỏi số đĩa nhiều nhất có thể chia là bao nhiêu ?
giúp mik zới mn ơi , mik cần gấp bài này . Mong mn sẽ giúp mik , cảm ơn mn nhìu
( 2x + 7 ) ⋮ ( x - 2 )
Giúp tui với mn ơi ! Cảm ơn mọi người rất nhiều