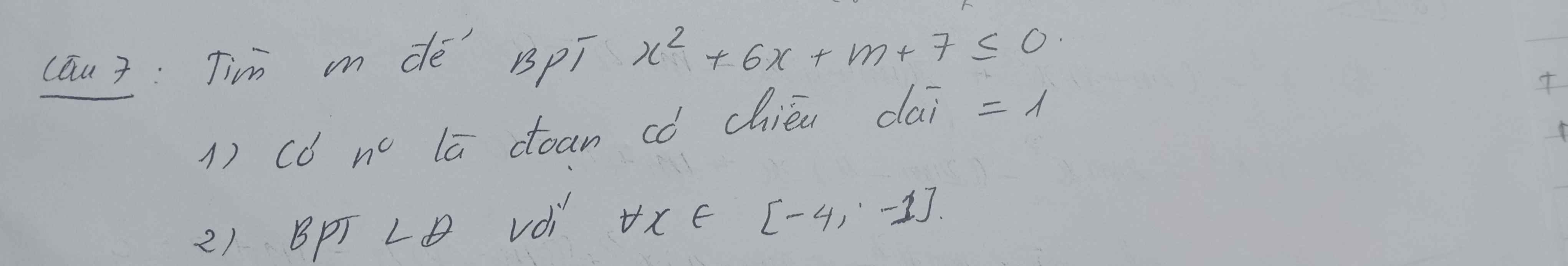a. Gọi \(x_1>x_2\) là 2 nghiệm của \(x^2+6x+m+7=0\) thì BPT đã cho có tập nghiệm là đoạn có chiều dài bằng 1 khi và chỉ khi \(x_1-x_2=1\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=1\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=1\)
\(\Leftrightarrow36-4\left(m+7\right)=1\)
\(\Leftrightarrow m=\dfrac{7}{4}\)
b. \(x^2+6x+m+7\le0\) ;\(\forall x\in\left[-4;-1\right]\)
\(\Leftrightarrow x^2+6x+7\le-m\) ; \(\forall x\in\left[-4;-1\right]\)
\(\Leftrightarrow-m\ge\max\limits_{\left[-4;-1\right]}\left(x^2+6x+7\right)\)
Xét hàm \(f\left(x\right)=x^2+6x+7\) trên \(\left[-4;-1\right]\)
\(-\dfrac{b}{2a}=-3\in\left[-4;-1\right]\) ; \(f\left(-4\right)=-1\) ; \(f\left(-3\right)=-2\) ; \(f\left(-1\right)=2\)
\(\Rightarrow\max\limits_{\left[-4;-1\right]}\left(x^2+6x+7\right)=2\Rightarrow-m\ge2\)
\(\Rightarrow m\le-2\)