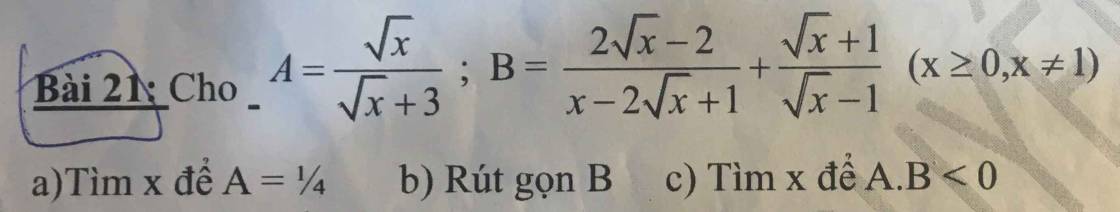a, đkxđ: \(x\ge0\)
\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}=\dfrac{1}{4}\Leftrightarrow\sqrt{x}+3=4\sqrt{x}\Leftrightarrow3=3\sqrt{x}\Leftrightarrow\sqrt{x}=1\Leftrightarrow\left(\sqrt{x}\right)^2=1^2\Leftrightarrow x=1\)
b,
\(B=\dfrac{2\sqrt{x}-2}{x-2\sqrt{x}+1}+\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{2\sqrt{x}-2}{\left(\sqrt{x}-1\right)^2}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)^2}=\dfrac{2\sqrt{x}-2+x-1}{\left(\sqrt{x}-1\right)^2}=\dfrac{\left(\sqrt{x}+1\right)^2-4}{\left(\sqrt{x}-1\right)^2}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-1\right)^2}=\dfrac{\sqrt{x}+3}{\sqrt{x}-1}\)
c,
\(A.B< 0\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+3}.\dfrac{\sqrt{x}+3}{\sqrt{x}-1}< 0\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-1}< 0\)
do \(\sqrt{x}\ge0\) mà \(\frac{\sqrt{x}}{\sqrt{x}-1}<0\Leftrightarrow \sqrt{x}-1<0\Leftrightarrow \sqrt{x}<1\Leftrightarrow x<1\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
x4 - x3 + x2 + 2
Mn giúp mình được không ạ. Nếu ai giúp mình giải được bài này thì mình cám ơn bạn đó nhé !
Mn giúp mình bài này vs ạ ?Cần gấp ạ
Mn ơi mn giúp mk bài này vs ạ (mình đang cần gấp🥺🥺🥺). Thanks mn.
giúp mình 2 bài này đc không ạ
Đọc tiếp
giúp mình 2 bài này đc không ạ
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ
mn ơi ai thấy bài này giúp em được ko ạ,e đang cần gấp lắm
Đọc tiếp
mn ơi ai thấy bài này giúp em được ko ạ,e đang cần gấp lắm
Giúp mình làm bài này được không ạ??
Khi nào xảy ra vòng lặp vô hạn?Giải thích và cách khắc phục
 mn giúp mik bài này với ạ này là hằng đẳng thúc ạ(ảnh hơi mờ mn thông cảm)
mn giúp mik bài này với ạ này là hằng đẳng thúc ạ(ảnh hơi mờ mn thông cảm)
Mn ơi mn giúp mk bài này vs ạ. Thanks mn.