a. Xét tam giác ABC và tam giác HBA, có:
\(\widehat{BAC}=\widehat{AHB}=90^0\)
\(\widehat{ACB}=\widehat{HAB}\) ( cùng phụ với \(\widehat{B}\) )
Vậy tam giác ABC đồng dạng tam giác HBA ( g.g )
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BH}{AB}\)
\(\Leftrightarrow AB^2=BC.AB\)
b.Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{15^2-9^2}=\sqrt{144}=12cm\)
Áp dụng t/c đường phân giác góc B, ta có:
\(\dfrac{AB}{AC}=\dfrac{AD}{CD}\)
\(\Leftrightarrow\dfrac{9}{15}=\dfrac{AD}{CD}\) \(\Leftrightarrow\dfrac{3}{5}=\dfrac{AD}{CD}\) \(\Leftrightarrow\dfrac{CD}{5}=\dfrac{AD}{3}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\dfrac{CD}{5}=\dfrac{AD}{3}=\dfrac{AD+AD}{5+3}=\dfrac{AC}{8}=\dfrac{12}{8}=\dfrac{3}{2}\)
\(\Rightarrow CD=\dfrac{3}{2}.5=7,5cm\)
\(\Rightarrow AD=\dfrac{3}{2}.3=4,5cm\)







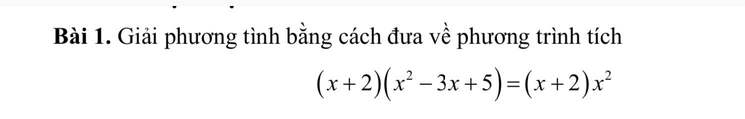

 vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều



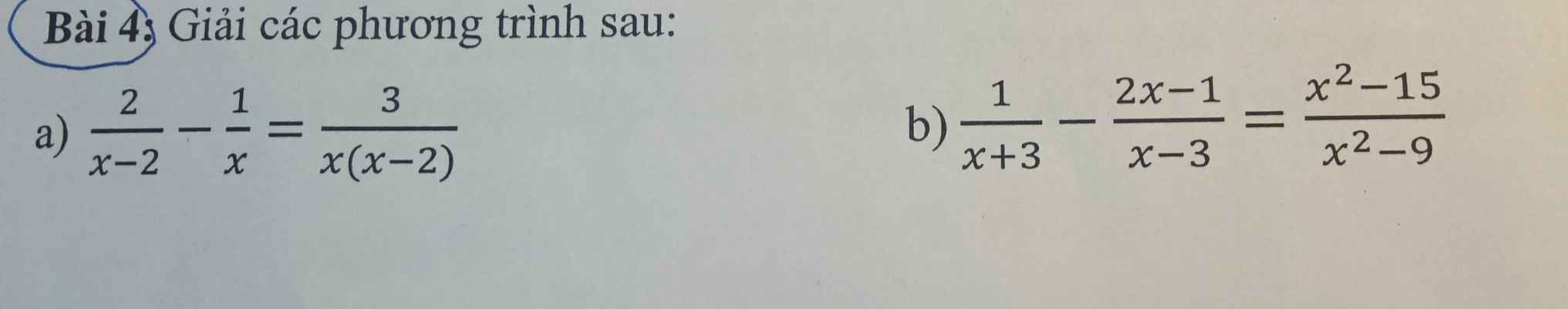
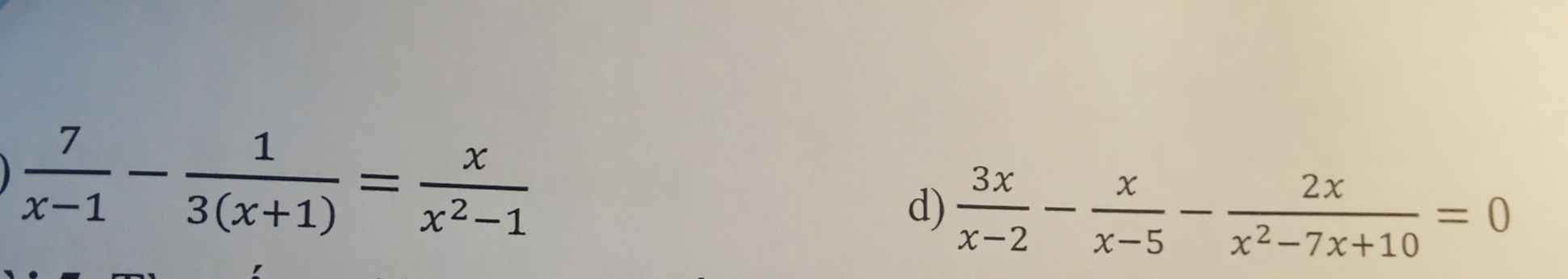 Mn giúp mik vs
Mn giúp mik vs